用时髦的话来讲，正态分布是一个“高性价比”的思考工具，因为它简单易学且应用广。正态分布广泛存在于自然界、社会科学、人文科学等领域，比如动物骨骼大小、考试成绩、产品质量指标、农作物产量等数据分布大多符合这一规律。在统计推断中，它是最重要的一类概率分布，也是许多统计方法的理论基础。
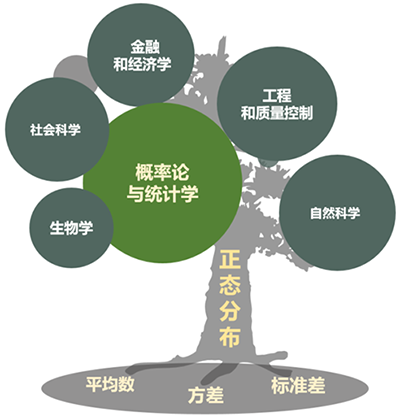
正态分布的背景知识
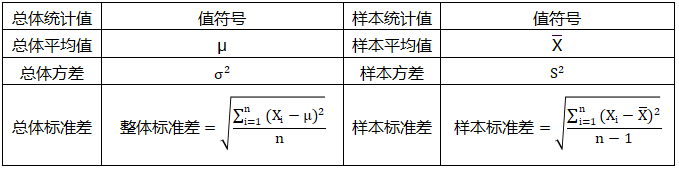
平均值、方差、标准差三个部分如同土壤，会很大程度影响正态分布这棵树的生长情况。因此，在介绍正态分布前，笔者需要简单介绍平均值、方差、标准差。
由于样本量的不同，平均值、方差、标准差可以分“总体”和“样本”两类。为强化对比，在后文的介绍中，笔者会在它们前面加上限定词，即“总体”或“样本”。如果没有限定词，那么平均值、方差、标准差所指代的就是总体的平均值、方差、标准差。
1、平均值
平均值(平均数)是的小学旧识。温故知新，因为它会在新情景下返场，用简洁、严谨、优美的数学语言，一句话回顾平均值：平均值是一组数据中所有数据之和再除以这组数据的个数，用于表示一组数据的集中趋势。例：1和10的平均值是这样计算的：(1+10)/2=5.5。
在正态分布中，由于样本量不同，平均值又可以分为总体平均值(μ)和样本平均值(
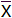)两类，两者的计算方法是一样的，只是符号有差异。【小贴士】希腊字母“μ”，发音为mu，是代表总体平均值的符号；“
”这个符号念作“X bar”，用于代表样本平均值。2、方差
方差是衡量一组数据波动大小的统计量。我们学习方差最重要的，不在于掌握繁杂的计算，而是能够根据其结果，了解所有数据的状态。
方差分为两类：总体方差和样本方差。两者的基本思路一致，但最大的差别在于样本量不同，前者是整体，后者是整体中的部分。
若X1，X2，X3......Xn的平均数为μ，则总体方差可表示为：
【小贴士】希腊字母“ ∑” 的小写形式为“σ”，英译音为Sigma，大小写符号都念“西格玛”。图片表示从1到n的多项求和。
我们还是用上面的1和10两个数字，总体平均值μ=5.5的简单例子，来看总体方差公式如何使用。(少量数据好计算，数据多的话，就让计算机/器帮忙吧。)
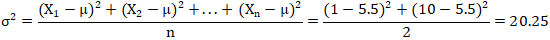
回到总体方差和样本方差区别的话题，这里举个简单的例子来说明。假设我们想知道中国人身高的标准差，但因人、财、物力有限，我们不可能把所有人都量一遍，因此，只能退而求其次，采取抽样策略，用样本标准差来推测整体，这时，我们就会用到样本方差。
样本方差和总体方差计算上略有区别，主要体现在分母上。不同于总体方差的分母为n，样本方差的分母为n-1。这里“-1”是为了修正样本方差对总体方差的估计偏差，这种现象被称为“贝塞尔校正”(Bessel's correction)。
这个减去的“1”，不特指任何一个数，它代表那个失去“独立客观”的维度(自由度)。
样本方差的计算公式如下：
因此，在计算样本标准差(S，即样本方差开根号)时，其分母也是n−1而不是n(即样本大小减1)。这里在后文标准差的部分还会提到。
【小贴士】样本标准差的分母为什么为n-1在数学领域已被证明，是较复杂的内容，这里不做过多展开，有兴趣的读者可查阅相关资料。
在公式的应用过程中，你或许会觉得计算很麻烦(事实也确实如此)。好消息是，计算在方差中并不是最重要的，我们要做的，是关注总体方差(σ²)的值，并由此了解方差想告诉我们的秘密：数据内部的状态如何。
在投资分析中，尤其是在股票投资中，方差是一个有用的统计工具，它可以帮助投资者了解投资组合的风险水平。同样的回报率，方差越小，则风险越低。
3、标准差
标准差(Standard Deviation)是方差的算术平均数的平方根，也用于反映一个数据集的离散程度。标准差实际上就是方差开根。
整体标准差用σ表示，样本标准差用S表示。两者的公式如图：
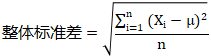
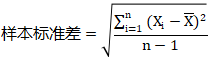
在本小节的末尾，我们来做个平均值、方差、标准差在“总体”和“样本”符号系统区别上的总结。详见下表：
当我们谈论一个正态分布时，通常是在谈论一个总体的分布，而不是一个样本的分布。因此，使用μ来表示正态分布的均值是合适的。
均值、方差、标准差的背景介绍已结束。别走开，下节更精彩，主角正态分布闪亮登场。
正态分布的主干知识
1、正态分布
正态分布一种常见的连续概率分布，它在自然科学和社会科学中常用于表示未知的随机变量。若随机变量X服从一个数学期望为μ、方差为σ²的正态分布，则记为N(μ，σ²)。
正态分布的曲线呈钟型，因此人们又经常称之为“钟形曲线”。正态分布虽有无数种形态，但仍由μ(平均值)和σ(标准差)两个数值决定。其中，μ决定了正态分布的位置，σ决定了分布的幅度。理解了这一点，你就不需要单独记忆每一个正态分布图啦。
现在，让我们一起来看一些有代表性的正态分布图吧(下面的文字浓度有点高，值得多看几遍)：
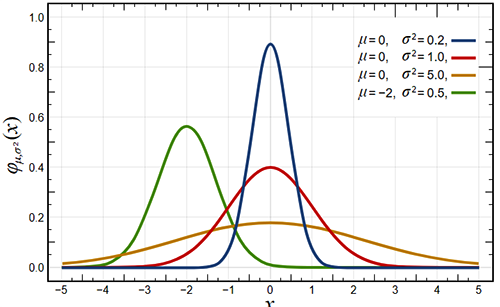
①当μ=0，σ=1时，这个正态分布就是标准正态分布，(见下图红线)。
②以正态分布为参考标准，μ为负则图形向左移动(见下图绿线)，反之，μ为正，则图形向右移动。
③μ不变，σ越小，则正态分布曲线越陡峭(见下图蓝线)，图像越“高瘦”，反之则越平缓(见下图黄线)，图像越“矮胖”。
【小贴士】不知道你是否注意到，和各行业一样，数学也有自己的业内术语，比如正态分布定义里的“服从”和“期望”。
数学语言中的“服从”是指“符合”、“遵从”的意思，一般指事物符合数学中的发展规律。
另外，数学术语中，“期望”或“数学期望”是一个重要的概念，特别是在概率论和统计学中。它表示随机变量的预期值或平均值。
除了上面的例子，正态分布其实还有数种形态，但它们的模型主要由μ(平均值)和σ(标准差)两个数值决定。
介绍了决定正态分布曲线的关键参数后，我们再来看看关于曲线下方覆盖面积呈现的规律。在距离平均值±1的标准差(即±σ)范围内，集中着约全体68.26%的数据；距离平均值±2的标准差(即±2σ)，集中着约95.45%的数据；距离平均值±3的标准差(即±3σ)，包含着99.73%的数据。曲线下方覆盖的面积，在统计学上被称“置信区间”。
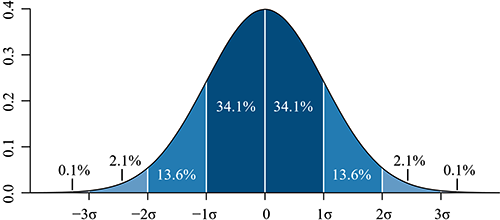
这张图是不是有点抽象？举几个例子，让置信区间中的数字走进生活。
①有大约68%的可能性，动态范围不超过平均值±σ。在一个班上，一班的平均分为80分，如果标准差为5分，我们就有68%的置信度说，考虑到随机性的影响，这个班的平均成绩应落在75~85之间，而不是之外。
②有大约95%的可能性，动态范围不超过平均值±2σ，即两个σ的置信度是95%。做科学试验时，通常需要有95%的置信度，才能得到大家认可的结论；在产品质检中，可以通过抽样检测来估计产品的平均质量水平，并利用95%置信区间来评估这个估计的可靠性。
③如果我们进一步扩大误差范围到±3σ，那么这个置信度就提高到99.7%。在要求极高的实验中，我们甚至会要求达到99.7%的置信度，甚至更高；在招聘中，面试官可以使用3σ原则来确定录取分数线。通过计算应聘者的平均分数和标准差，可以确定一个合理的分数线范围，从而筛选出合格的应聘者。
【小贴士】总体正态分布图vs样本正态分布图(符号区别)
正态分布的标准化
在正态分布的主干知识中，我们介绍了影响正态分布形态的土壤(平均值、方差、标准差)，以及由此长出的小树(正态分布的图像)。
1、标准化与查表求概率
虽然通过观察图也能把握大致情况，但计算数值后会更便于理解，也方便向他人展示。好消息是，Z转换(标准化)可以实现统一尺度。
对于数据集中的每一个数值X，可使用以下公式进行标准化：
在这个公式中，Z是转换后的标准值，X 是原始数据点的值，μ是原始数据的平均值和σ是原始数据的标准差。
别被公式吓到，放进日常的简单应用场景就豁然开朗了。
小A参加了小学模拟考试，数学得了73分，英语得了76分。数学平均分是60分，英语平均分是68分。那么，小A的数学成绩和英文成绩，哪一个相对来说比较好呢？(得分均按照正态分布)实际上，仅这些条件是无法进行判断的，还需要能够表示全体离散程度的标准差。现在，我们假定数学是标准差为8分的正态分布，英语则是标准差为6分的正态分布。
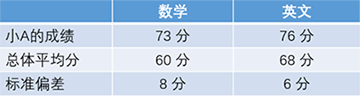
用Z变换的公式可得：
数学 : (得分-平均分)÷标准差=(73-60)÷8=1.625
英语 : (得分-平均分)÷标准差=(76-68)÷6=1.333
也就是说，当标准差为1时，小A的数学、英语成绩标准差分别是1.625、1.333。不同学科的成绩转化为标准得分后，变得可比较了。
另外，用“标准得分=1”进行了标准化，“平均值”会变成什么样呢？本来，平均分根据科目的不同而不同，但以标准得分进行分布的时候，平均值为0。
因此，在对成绩进行“标准化”时，分布会变为平均值=0、标准差=1的标准正态分布。需注意的是，标准化改变的只是图的位置，比如向左或向右平移，但并不会改变“高矮胖瘦”。
完成Z变换，我们就通过可以利用z值表找到对应的概率值啦。这里会用到“标准正态分布表”。
这个表是前人整理好的数据，用起来也很方便。首先，我们要看最左手列，去查阅Z至小数点后1位数，之后，我们再查最上一行，看Z的第二位小数，左右交叉得到的数，就是我们需要找的数。
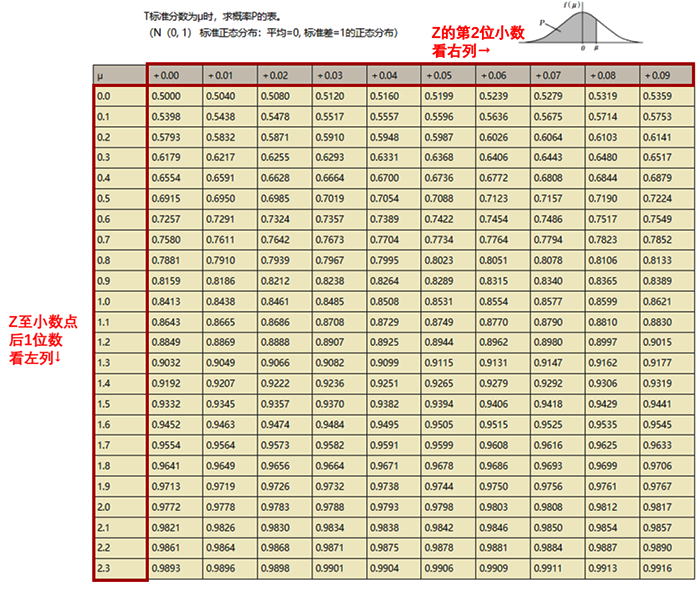
放到小A的例子中，数学的标准差为1.625、英语的标准差为1.333。我们来试试查这个表。以数学为例，先看最左列，Z至小数点后1位数为1.6，接着，再看最上行，Z的第2位小数我取0.02，交叉得到的数就是0.9474(蓝色方框中的数)。英语的查阅方式同理，取值为0.9082。
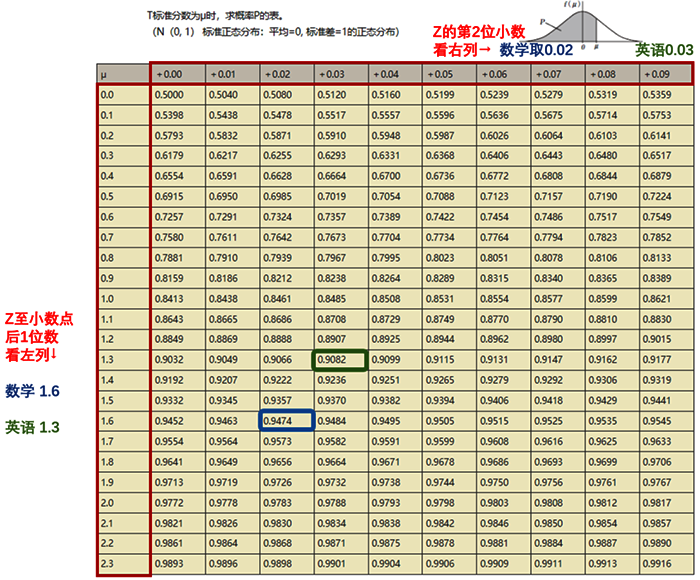
查表后，就是分析数据了。数学取值为0.9474，英语为0.9082，即数学约处于94.74%的水平，英语处于90.82%的水平。如果参加全国数学、英语模拟考试的人有1万人，小A数学大概处于526名的位置((1-0.9474)×10000=526名)，英语处于918名的位置。用图表示更清晰，这里以数学为例：
恭喜看到这的你，在20分钟左右的时间，你已经了解了正态分布最核心的知识！
最后，请让我们为你做个简要的总结：我们先一起回顾了平均值、方差和基本差的背景知识，并在此基础上了解了正态分布的形状、特征以及如何使用。
