
图1 反向对象控制模型分析
τ=7.03-1≈6s
T=13.7-7.03≈6.7s

根据切线数据可以知道被控对象的PID控制模型:稳态系数,增益K=1;动态系数,时间常数T=6.7s;时间滞后,纯滞后时间τ=6s。
PID控制器参数计算如下:
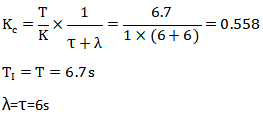
使用这组PID参数进行设定值阶跃变化,闭环响应曲线如图2所示。从设定值阶跃响应曲线可以确定:Lambda整定方法只需要从响应曲线获得一阶纯滞后控制模型参数就能准确得到最优的PID参数。

图2 反向对象设定值阶跃响应曲线
Lambda整定方法适用于欠阻尼、大纯滞后、非最小相位等各类被控对象,可以作为PID参数整定标准化的基础。








