如果选择λ=T=1s,根据Lambda整定方法得到的PID参数如下:
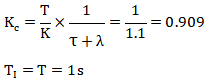
如果选择最强参数λ=τ=0.1s,根据Lambda整定方法得到的PID参数如下:|
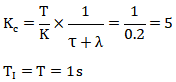
λ=1s和λ=0.1s的设定值阶跃响应如图1所示。

图1 小纯滞后对象不同λ时的设定值阶跃响应
λ=T=1s时,根据PID控制器输出的曲线可以看出设定值阶跃响应速度基本上和开环响应速度一致,这是λ=T的结果也符合预期。
如果选择λ=t=0.1s,设定值阶跃响应速度只需要0.3s即可达到设定值。所以我们称λ为期望闭环时间常数。λ越小闭环时间常数越小,闭环响应速度越快。λ越大闭环时间常数越大,闭环响应速度越慢。而且期望闭环时间常数λ最小值和纯滞后时间τ有关。
对于小纯滞后被控对象,选择最强PID参数,设定值阶跃变化时也不会振荡。但是如图1(b)所示此时控制器的输出变化会比较大,瞬时的PID控制器输出大幅度变化在很多情况下都是不允许的。甚至选择λ=T=1s时,如果设定值大幅度变化也会导致PID控制器输出大幅度变化。
因为增加λ也会影响控制系统抑制干扰的能力,所以小纯滞后对象不建议更大幅度地增大λ而是选择比例先行PID或者限制设定值的变化速度。在闭环系统稳定的前提下,如何合理地选择λ也是PID参数整定需要综合考虑的地方。也有的资料认为在大时间常数对象中可以使用微分来改进控制性能,但实际上我们总可以通过设置不同的λ来获得期望的控制性能,所以大时间常数对象也不需要使用微分。








