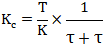可以保证设定值阶跃响应有超调无振荡。通过多次的设定值阶跃响应可以得到和前面一样的结论：纯比例控制器总是有余差。为了消除余差，可以使用比例积分控制器。积分作用通过对偏差的累积消除余差，偏差累积的速度应该和被控对象的动态特性时间常数相匹配。我们使用基准模型、Kc=0.25和不同积分时间进行闭环设定值阶跃测试。设定值阶跃响应曲线如图1所示。当积分时间太小(积分作用太强)时，设定值阶跃响应会超调甚至振荡。当积分时间太大(积分作用太弱)时，设定值阶跃响应缓慢，表现为“拖尾”现象。合适的积分时间应和被控对象的时间常数匹配。
基于上面的信息综合考虑，自衡对象的比例积分控制器整定公式如下式所示：
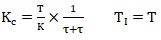
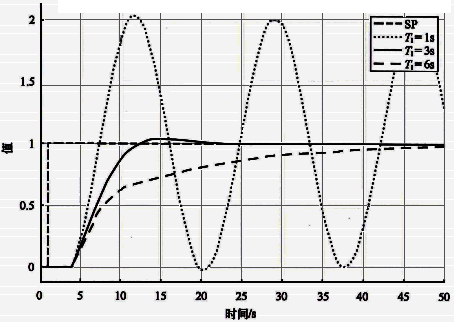
图1 基准模型和K=0.25，不同积分时间设定值阶跃响应
基于上面的信息综合考虑，自衡对象的比例积分控制器整定公式如式所示：
使用这个整定公式
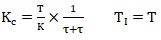，对纯滞后主导自衡对象(K/T/τ=5/0.1s/10s)和时间常数主导自衡对象(K/T/τ=5/10s/0.1s)进行控制。根据自衡对象的比例积分控制器整定公式计算的PID参数分别为：Kc/TI=0.001/0.1s和Kc/TI=10/10s。两个自衡对象的闭环设定值阶跃响应分别见图2和图3。使用该整定方法确定的PID参数，可以实现对这两个典型自衡对象的有效控制，而且无论是哪种自衡对象过程变量都表现为有超调无振荡的最优性能。对纯滞后主导对象而言，积分作用很强只要比例作用合适也能实现最优控制。对时间常数主导自衡对象而言，该整定方法提供的比例作用太强了，控制器输出变化明显太大。
图2 K/T/τ=5/0.1s/10s和Kc/TI=0.001/0.1s设定值阶跃响应
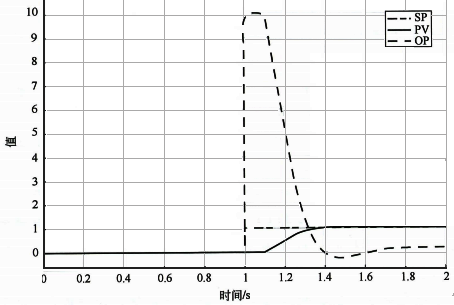
图3 K/T/τ=5/10s/0.1s和Kc/TI=10/10s设定值阶跃响应
