为方便大家深入了解PID算法,快速掌握PID参数整定方法,昌晖仪表在本文分享PID形式、两自由度PID、不完全微分、积分饱和和变比例增益PID方面的专业知识,希望对你有所帮助。
1、PID形式
本文中使用的PID形式又称为非交互式PID算法、ISA形式、标准形式或理想形式。昌晖仪表后面的分析都是基于这种形式的PID算法。标准形式的PID算法在文章《PID参数影响分析》详细介绍过,标准PID控制算法的微积分方程为:
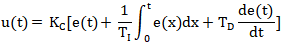
既然有图1所示的非交互式PID,就有图2所示的交互式PID,而且交互式PID出现得更早,是早期PID应用的主要形式。
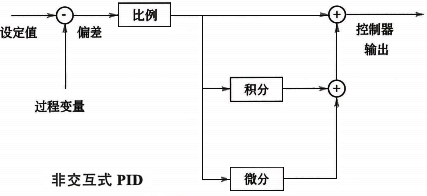
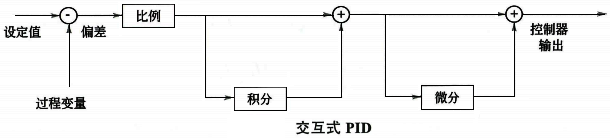
最初的PID算法都是基于某些气动和机械设备设计的。比例控制是当时占主导地位的控制技术,PID控制器经过模块化设计,使得积分作用和微分作用是控制器中独立的硬件模块,除了纯比例作用之外,使用积分作用和微分作用模块还要付出额外的成本。实现积分作用和微分作用的最简单方法是一种恰好对控制器增益具有交互作用的方法,这种形式也称为串联形式。换句话说,这种算法形式是为了简化控制器的物理设计而做出的一种折中。串联形式PID控制器的微积分方程为:
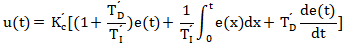
式中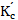 为交互式PID控制器的比例增益;
为交互式PID控制器的比例增益;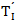 为交互式PID控制器的积分时间;
为交互式PID控制器的积分时间;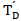 为交互式PID控制器的微分时间。
为交互式PID控制器的微分时间。
交互式PID控制器总是可以表示为非交互式PID控制器,其系数为:
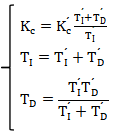
交互式PID控制器,对应于非交互式PID控制器,当且仅当:TI≥4TD,那么:
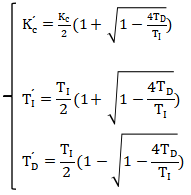
早期的气动控制器使用交互式PID更容易构建。遵循惯例是很多控制系统一直保留着交互式PID的原因。
不同的控制系统可能有不同形式的PID。这意味着,如果控制回路中的控制器被另一种类型的控制器所取代,则可能需要重新计算控制器参数以保证闭环性能不变。PID控制器只有同时使用积分作用和微分作用时,交互式和非交互式才不同。如果PID控制器只用作比例、比例积分或比例微分控制器,这两种形式等价。
PID算法的另一种形式是并联式,其微积分方程为:
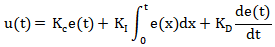
式中Kc为并联式PID控制器的比例增益; KI为并联式PID控制器的积分增益;KD为并联式PID控制器的微分增益。
并联式PID等价于标准形式PID,但参数值有很大的不同。这可能会给没有意识到差异的人带来麻烦,特别是参数KI被称为积分时间、参数KD被称为微分时间时。因为参数是独立出现的,所以并联式PID所给出的形式在解析计算中是有益的。这种表示法还有一个优点,就是可以通过参数设置获得纯比例、纯积分或纯微分作用。
下面是并联式PID参数与标准形式PID参数的关系:
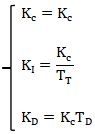
综上所述,实际应用中有三种不同形式的PID控制器:①标准式或非交互式;②串联或交互式;③并联式。
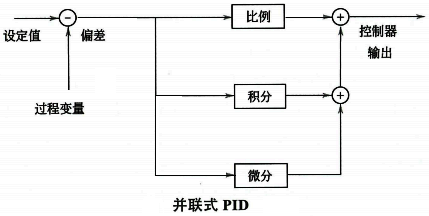
标准式有时被称为ISA形式或理想形式。比例作用、积分作用和微分作用在时域中是互不影响的。并联式是最一般的形式,因为纯比例或纯积分作用可以用参数设置得到,是最灵活的形式。然而,它也是一种参数几乎没有物理解释的形式。
2、两自由度PID
PID控制系统的特点是形成一个偏差,即设定值和过程变量之间的差值:控制器通过对偏差处理产生控制器输出,然后将控制器输出作用到过程中。因为控制器是基于偏差运算的,所以这样的系统被称为“偏差反馈系统”。实践经验和科学分析都表明抗扰最强的PID参数,设定值阶跃变化时闭环控制系统会振荡,通过将设定值和过程变量分开处理,可以得到一种更灵活的结构来解决这个问题。式给出了PID控制器的改进形式-两自由度PID控制器。
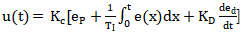
比例部分的偏差: eP=b×SP-PV, 式中,e为比例部分偏差;b为比例作用设定值加权系数。
微分部分的偏差:eD=c×SP-PV, 式中,eD为微分部分偏差;c为微分作用设定值加权系数。
积分部分中的偏差必须是真正的偏差:e=SP-PV。
为了避免稳态偏差,不同的b和c值所得到的控制作用将以相同的方式响应负载扰动和测量噪声。然而,对设定值阶跃变化的响应将取决于b和c的值。b=0和c=0时,只在积分项中引入设定值信息,对设定值阶跃变化的响应最平缓。
参数c通常选择为零,以避免微分作用于设定值时,控制输出由于设定值的阶跃变化而出现大的瞬时变化。
b=0和c=0的控制器被称为I-PD或者比例微分先行,b=1和c=0的控制器被称为PI-D或者微分先行。选择b=0时,设定值跟踪性能可能不能满足要求。如果既关注设定值跟踪性能又关注抗扰能力,可以选择O≤b≤1和较强的PID参数,考虑到设定值阶跃变化时的响应特性,推荐b=0.5。
一般来说,一个控制系统有许多不同的要求。它应该对设定值的变化有良好的瞬态响应,并且能够克服负载扰动和测量噪声,而且控制器输出不能过度动作。对于只有偏差反馈的系统,尝试用相同的机制来满足所有的要求,这样的系统称为单自由度系统。两自由度PID通过为设定值和过程变量设置不同的信号路径,有更大的灵活性来满足控制要求。微分作用加权系数c往往选择为0即可。比例作用加权系数b则需要根据PID参数和设定值跟踪的要求综合评判。如果PID参数整定得非常弱又想改进设定值跟踪能力,b也可能大于1,这种选择要非常谨慎。
3、不完全微分
如果存在高频测量噪声,理想微分作用会使控制器输出高频大幅振荡。因此微分项的高频增益应受到限制,以避免这个问题。这可以通过如下方式修正微分作用来实现:
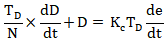
式中,D为微分作用;N为微分增益。
这种修正可以解释为理想微分被一个时间常数为TD/N的一阶系统滤波,这个近似作为低频信号分量的微分。而增益最大限制为KcN,这意味着高频测量噪声最多被放大KcN倍,N的典型值为8~20。
实际工业PID控制器中大多使用不完全微分,不完全微分的微分时间的影响和理想微分形式的微分作用显著不同。引入不完全微分后,微分输出在第一个采样周期的脉冲高度下降,然后按一阶过程逐渐衰减。所以不完全微分有效地克服了理想微分形式的缺点,具有更好的实用特性。微分作用最初被称为“预作用”实际上就是不完全微分。理想微分不完全化可以理解为理论到实践的具体可行实现,不完全微分的理想化处理可以理解为从实践到理论的抽象。理论和实际的差别增加了微分作用整定的难度。
4、积分饱和
所谓积分饱和现象,是指若系统存在一个方向的偏差,PID控制器的输出由于积分作用的不断累加而加大,从而导致最终控制元件达到极限位置。此后若控制器输出继续增大,最终控制元件也不会再增大,即系统输出超出正常运行范围而进入了饱和区。一旦出现反向偏差,最终控制元件逐渐从饱和区退出。进入饱和区越深,则退出饱和时间越长。此段时间内,最终控制元件仍停留在极限位置而不能随着偏差反向立即做出相应的改变,这时系统就像失去控制一样,造成控制性能恶化。这种现象称为积分饱和现象。
模拟PID控制器制造商发明了一些技巧来避免积分饱和。这些技巧通常被视为商业机密,很少被提及。在数字PID控制器时代,当控制器算法的输出超过范围时可以只取边界值,如果采用增量型或速度型算法,每次计算出应调整的增量值,当控制作用量将超过额定高低限值时,则保持在高限值或低限值,这样当偏差减小或改变方向时,控制器输出就能更快脱离高限值或低限值。所以增量形式的PID算法基本上不会出现积分饱和现象。
5、变比例增益PID
在先进控制里有个非常重要的范围控制的概念。简单说就是过程变量在范围高低限以外时首先把过程变量控制到范围内,等过程变量回到范围内后,如果没有优化要求则操纵变量停止控制作用,如果过程变量还有一个最优的目标,则可以缓慢的速度(例如六分之一的控制速度)进行优化。优化的方向有时候和控制的方向相反,使用更慢的优化速度可以确保优先进行控制。在PID控制回路中使用变比例增益PID来实现。

式中,Kgap为控制器最终增益;Cgap为变增益系数。
当Cgap=0时,过程变量进入范围后操纵变量停止控制,此时也称为死区PID。当Cgap=1/6时,过程变量进入范围后以1/6的控制速度向设定值优化。这个设定值可以固定不变,也可以来自其他控制回路。变增益PID有效地提高了控制性能,降低了范围内的优化速度。








