在石油、化工、冶金、电力、轻工和建材等工业生产中,连续的或按一定程序周期进行的生产过程的自动控制称为生产过程自动化。凡是采用模拟或数字控制方式对生产过程的某一或某些物理参数进行的自动控制就称为过程控制。过程控制一般使用数学方法对系统进行研究,并使用微分方程来建立这些过程的数学模型。微分方程是包含变量微分的方程。微分方程的阶次是方程中包含的变量的最大微分阶次。一个过程的阶次就是对其建模所需的微分方程的阶次。
过程阶次是一个重要的概念,因为它描述了过程如何响应PID控制器输出作用。幸运的是,我们不需要钻研数学知识来获得实际过程的阶次,只需对过程进行阶跃测试,过程阶跃响应曲线会告诉我们所需要的信息。
在过程变量稳定后,通过控制器输出的阶跃变化获得响应曲线。响应曲线揭示了被控过程的动态特性。响应曲线是系统在控制器输出阶跃变化作用下,过程变量从初始状态到稳定状态相对于时间的曲线。
一阶过程
图1是一阶过程的响应曲线。该响应曲线描述了控制器输出变化5%时,过程变量从初始状态到稳定状态的动态响应过程。
理解一阶纯滞后过程模型是理解PID控制的基础。了解一阶纯滞后过程 的三个表征参数-纯滞后时间τ、时间常数T和增益K,将极大地有助于整定PID控制器,因为这也是进行PID参数整定计算的控制模型参数。
一阶过程对过程输入阶跃变化具有指数响应,并且可以完全由三个参数表征:纯滞后时间τ 、时间常数T和增益 K。

图1 一阶纯滞后过程响应曲线
1、纯滞后时间
纯滞后时间τ是从控制器输出变化到过程变量开始发生变化之间经过的时间。
纯滞后是指由于对象的测量环节、传输环节或其他环节造成整个系统输出纯滞后于输入变化的现象。传感器和最终控制元件都可能增加过程纯滞后时间,而过程本身的纯滞后时间通常是传输延迟的结果(如传送带上输送的物料、管道中的可压缩物料)。纯滞后时间是回路整定的“敌人”,一个过程中纯滞后时间的长短将决定该过程能被整定到什么程度并保持稳定。
2、纯滞后时间计算
如图1所示,控制器输出在1s时发生了阶跃变化,直到8s,过程变量才开始变化。本例中的纯滞后时间τ为:τ=8-1=7s。
控制器看到的纯滞后时间是传感器、最终控制元件和过程自身纯滞后时间的总和。
3、时间常数
时间常数T描述了控制器输出变化时过程变量的响应速度。时间常数是阶跃变化时一阶过程响应中过程变量开始变化到首次达到其总变化量63.2%的时间。
时间常数越小,过程越快。需要注意的是过程变量响应的开始时间为过程变量变化的第一反应时间,而不是控制器输出第一次变化的时间。不同时间常数倍数时对应的过程变量变化与总变化量的关系见表1。理论上达到稳态的时间无穷大,一般认为3倍时间常数后一阶过程响应达到过程变化量的95%就算进入稳态。
表1 时间常数与变化量/总变化量的关系

4、时间常数计算
为了找到一阶纯滞后过程的时间常数,必须找到阶跃变化响应过程中63.2%的过程变量变化,并从响应曲线中确定这个过程变量值出现的时间。
如图1所示,在控制器输出阶跃变化之前,过程变量值稳定在0。阶跃变化后,直到8s,过程变量才开始变化,然后逐渐稳定在10。我们使用符号△来表示变化,△PV是过程变量的变化。
一倍时间常数后的过程变量的变化为: ,一倍时间常数后的过程变量值为:0+6.32=6.32
,一倍时间常数后的过程变量值为:0+6.32=6.32
从图1的响应曲线中,我们可以看到在13s时的过程变量达到6.32。 时间常数T是这个时间减去过程变量开始变化的时间:T=13-8=5s
控制器看到的过程时间常数T是传感器、最终控制元件和过程自身时间常数的函数。
5、过程的可控性
纯滞后时间和时间常数之间的关系,决定了过程的可控性。纯滞后时间小于时间常数(纯滞后时间/时间常数<1)的过程更容易控制。纯滞后时间大于时间常数(纯滞后时间/时间常数≥1)的过程更难控制,控制器必须整定得弱一些从而保持闭环系统稳定。
图1的过程中, ,因此该过程相对难控制。
,因此该过程相对难控制。
“大纯滞后过程闭环稳定,控制器参数可调范围更小,所以相对而言更难控制”,这个传言是由于早期的控制器参数整定方法不适用于大纯滞后过程而产生的。实际上通过使用最新的控制器参数整定方法,针对大纯滞后过程也能很容易地找到闭环稳定的控制器参数。但是大纯滞后过程控制器参数的闭环稳定区域的确显著变小,所以传言说的也没有错。直接使用统一公式可以轻松地得到大纯滞后过程稳定快速控制的PID参数。
6、增益
增益K是过程变量变化对控制器输出变化的响应倍数,或过程变量的稳态变化除以控制器输出的稳态变化。增益是一个描述过程输入变化导致过程变量变化幅度的模型参数。增益可以通过用过程变量稳态变化除以引起该变化的控制器输出稳态变化得到。增益反映了过程的稳态特性。
7、增益计算
图1中过程变量的变化△PV是:
控制器输出的变化△OP是:
这个过程的增益是:
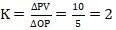
8、无单位增益
在这个过程中有一个重要的知识点:上面计算的增益其实是带单位的,与大多数软件模拟不同,实际使用的控制器增益都是无单位的。所以进行PID参数计算时也要对增益进行无单位处理。当增益用于计算实际使用的PID控制器参数时,过程变量的变化需要用过程变量量程的百分比表示,控制器输出的变化也需要用控制器输出量程的百分比表示,因为实际使用的控制器计算使用的偏差是无单位形式。
在本例中,过程变量的量程范围为0~100,过程变量量程为100-0=100。过程变量变化占量程的百分比为:

控制器输出的量程范围为0~100,控制器输出量程为100-0=100。控制器输出变化占量程的百分比为:

无单位增益:

将增益转换为无单位增益的快捷方法是使用以下计算:
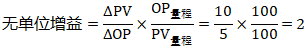
高阶过程
与一阶过程不同,高阶过程对控制器输出阶跃变化表现出高阶特性响应。
高阶特性响应可以分为三类:过阻尼、欠阻尼和临界阻尼。
任何一个振荡系统,当阻尼增加到一定程度后,物体的运动是非周期性的,物体振荡连一次都不能完成,只是慢慢地回到平衡位置就停止了。 一个系统受初始扰动后不再受外界激励,因受到阻力造成能量损失而位移峰值逐渐减小的振荡称为阻尼振荡。系统的状态由阻尼率ξ来划分。
①当0<ξ<1时,系统所受的阻尼力较小,要振荡很多次且振幅逐渐减小,最后才能达到平衡位置的情况,称为“欠阻尼”状态。
②当ξ=1时,阻尼的大小刚好使系统做无超调运动,即阻力使振荡物体刚好能没有超调而又能最快地回到平衡位置的情况,称为“临界阻尼”状态。
③当ξ>1时,系统所受的阻尼力较大,阻尼使系统做无超调运动,即阻力使振荡物体不做周期性振荡且更慢回到平衡位置的情况,称为“过阻尼”状态。
三类高阶特性响应曲线如图2所示。实际生产过程中大部分被控对象都具有过阻尼特性,有时候也称这类过程为多容过程。临界阻尼特性和欠阻尼特性在生产过程中不常见。
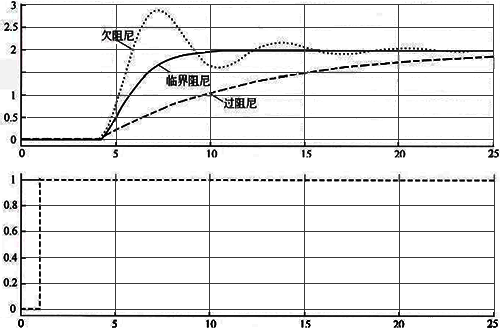
图2 高阶纯滞后过程响应曲线
过阻尼的高阶过程看起来很像一阶纯滞后过程。一阶和高阶过阻尼过程的区别是对阶跃变化的初始响应。与高阶过程相比,一阶过程在纯滞后时间过后对控制器阶跃变化具有更清晰的响应。一般来说,过程阶次越高,响应曲线越呈“S”形,对阶跃变化的初始响应越缓慢。图3显示了过阻尼二阶和三阶过程的响应曲线与一阶过程响应曲线的区别。
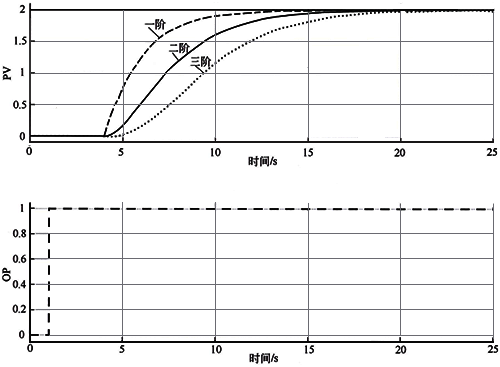
图3 过阻尼高阶纯滞后过程响应曲线








