在一般的轴承选型综合型录里都有将轴承受力折算成当量负荷的计算方法介绍,但是经常没有轴承受力计算的部分。最近经常有工程师提问关于轴承受力计算的问题,因此撰文阐述。
轴承系统受力方向
一般的轴系统都是有两个定位支点固定的,我们将一根轴的三维空间用三个相互垂直的空间坐标轴描述:轴向a,径向x,径向y。其中轴向是和轴线方向一致的方向,x,y分别是轴系统径向平面内相互垂直的两根坐标轴。(径向平面就是轴半径圆所处的平面,与轴向平面相垂直)如下图所示:
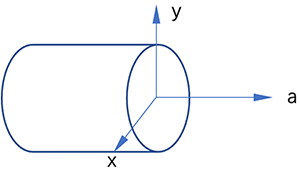
在这样的坐标系统下,轴承安装在轴上,轴承半径平面在上图中的径向平面上,因此轴承受到的力可以被分解为这三个方向上的分力。轴承在径向平面上x,y方向的力可以合成为一个径向合力。通常对于轴承而言,进行校核计算的时候,不论径向合力在径向平面上的那个角度上,对于一般的滚动轴承而言,均可以接受,因此我们不太关心具体角度,所以也不必将这个力分解为x,y方向的,直接合成为径向力Fr即可,同时对于轴向力我们用Fa表示。所以,在对轴承进行受力分析的时候,一般计算出径向力和轴向力即可。
轴承在轴系统中的受力分析方法
对于一个双支点支撑的轴系统,可能受到各种方向的力,因此进行受力分析之前,需要将各个方向的受力折算到x,y,a三个方向上,然后计算这三个平面上轴承的受力,最后将轴承径向平面的受力合成为一个径向负荷。这就是轴承受力分析的基本思路。
我们用一台卧式电机受力举例说明。首先,对于一台卧式电机而言,如果轴伸端存在一个径向负荷,那么电机受力如图所示,这个例子中我们将重力G和径向负荷设置在同一个平面上,因此省去了合成的计算过程。在工程实际中,情况往往不同,那么就按照上述方法进行里的分解合成,最终计算轴承受力:
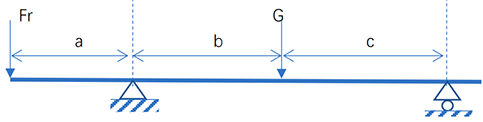
此时电机转子重力G作为径向力存在,负荷与轴承的距离分别为a,b,c。轴系统运行的时候,除了周向保持自由旋转,其他方向全部稳定,因此可以根据力矩平衡计算两个轴承的受力。我们称左边轴承为1号轴承,右边为2号,以1号轴承为支点的力矩平衡方程为:
Fr×a=G×b-Fr2×(b+c)
因此可以计算右边轴承的径向负荷
Fr2=(G×b-Fr×a)/(b+c)
此时,Fr1+Fr2=G+Fr。因此有Fr1=G+Fr-Fr2。
当然,Fr1也可以根据力矩平衡进行计算。
电机中如有轴向力,则定位端轴承(左边轴承)承受此轴向负荷,而右边浮动端轴承轴向负荷为0。
倾覆力矩
有工程师提问关于倾覆力矩对轴承受力的影响,并且在资料里找不到计算方法,因此求助。我们依然观察上面的例子,事实上径向负荷Fr不仅是一个径向负荷,径向负荷Fr对于bc段轴系统而言,也构成一个Fr×a的倾覆力矩。所以不难发现计算方法与上述计算无异。
在一些情况下的轴系统倾覆力矩是一对力偶矩。此时如果用一般的手工计算,默认系统为刚性系统,此时力偶矩在自身所在平面上相互抵消。但是如果考虑系统挠性,那么情况就复杂的多,此时建议使用一些更高级的计算方法分析轴承受力,上述介绍的一般手算方式就不适合这种场合。








