本文以自衡对象Lambda整定和非自衡对象Lambda整定为主要内容,在大家阅读正文之前,大家有必要先回顾一下什么是自衡对象和积分对象?什么是Lambda整定?概念清楚就可以阅读正文了。
自衡对象Lambda整定
使用Lambda整定的第一步是计算。闭环时间常数描述控制器响应设定值阶跃变化时的速度。因此,一个小的闭环时间常数(即短响应时间)意味着一个积极的PID调节器或一个以快速响应为特征的PID调节器。
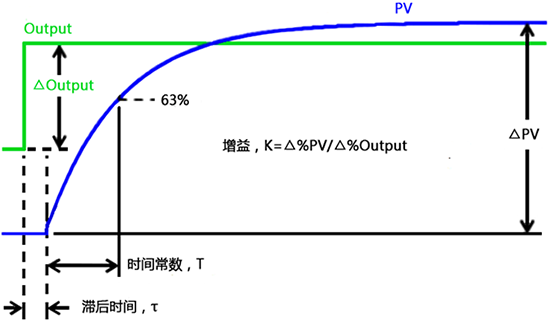
图1 闭环时间常数
被控对象:

可使用以下公式确定自衡对象的PID整定参数:


当λ=τ,闭环的设定值跟踪会超调。这也是Lambda整定方法推荐的最强控制作用。当λ=2τ时,闭环设定值跟踪不振荡。Lambda整定推荐的鲁棒参数为λ=3τ。
在实际使用中,如果被控对象不是标准的一阶纯滞后特性,lambda整定方法如何使用呢?在实际对象中,无论是如图2的多容对象还是如图3的欠阻尼对象。都使用统一的方法获得Lambda整定需要的模型时间常数T和纯滞后时间τ。
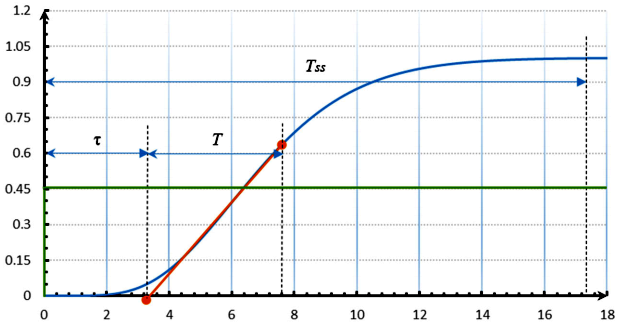
图2 多容对象开环响应
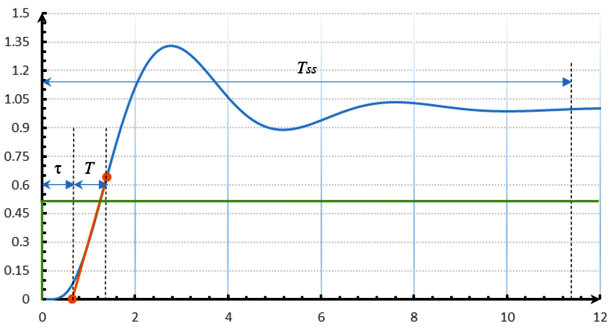
图3 欠阻尼对象开环响应
对于自衡对象而言,模型增益无论使用开环测试还是闭环测试,其计算公式都一样:
要注意模型增益计算数据可能受到干扰的影响,建议多次测试并选择大的模型增益进行控制器整定参数计算。
从开环响应的63.2%ΔPV,沿响应曲线向前做响应曲线的切线,切线与时间坐标轴相交。输出变化到交点为纯滞后时间τ,交点到63.2%ΔPV的时间为时间常数T。
考虑被控对象的复杂性,推荐λ:

其中Tss为稳定时间,稳定时间为阶跃开始时到PV稳定时的时间。Lambda整定参数为:


非自衡对象Lambda整定
非自衡对象的Lambda是克服扰动的闭环停止时间。闭环时间常数描述控制器克服扰动的速度。因此,一个小的闭环时间常数值(即短响应时间)意味着一个积极的PID调节器。

被控对象:
可使用以下公式确定积分对象的PID整定参数:

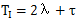
非自衡纯滞后过程的λ为负载扰动的最大偏差时间。如果目标是最大抗扰能力,则选择一个较小的λ。如果目标是允许被控变量变化并减少控制器输出和利用容器吸收被控变量的波动,则选择更大的λ。λ没有上限但是λ必须足够小,才能将被控变量保持在最大干扰时的允许偏差范围内。
建议的最小λ为1倍的纯滞后,这是最强的PID参数。此时的PID参数如下:
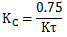

使用这组PID整定参数时,设定值变化的测量值响应为有超调无振荡。液位控制回路振荡的常见原因是比例系数和积分时间的乘积不够大。对于汽包液位控制而言,纯滞后主要来自“虚假液位”,这增加了锅炉汽包水位控制的难度。








