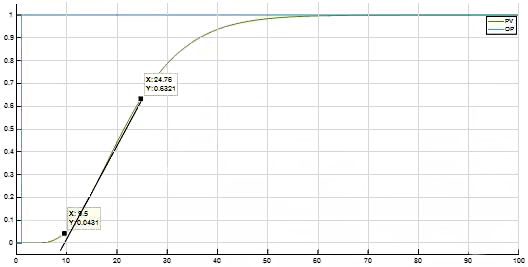
图1 被控对象开环输出单位阶跃响应
使用自衡对象的Lambda整定方法进行参数整定。
从开环响应的63.2%ΔPV,沿响应曲线向前做响应曲线的切线,切线与时间坐标轴相交。输出变化到交点为纯滞后时间τ,交点到63.2%ΔPV的时间为时间常数T。被控对象的模型参数为:K=1;T=24.76-9.5=15.26;τ=9.5-1=8.5
考虑被控对象的复杂性,推荐λ:
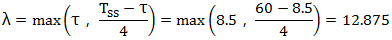
按Lambda方法可以计算得到PID的PI参数:
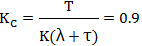

由于被控对象有明显的多容特性,可以选择微分TD=τ/2=4.25,我们选择TD=0、TD=4.25、TD=4.25且采用PI-D形式分别闭环设定值阶跃响应。当TD=0,测量值表现出振荡的特性,这说明对于复杂的被控对象λ选择的稍微大点对闭环响应的稳定更有利。当TD=4.25测量值的瞬时响应明显变快,但是微分在靠近设定值时的抑制能力明显增强,总体表现出控制作用略微不足的现象,另外由于微分的存在当设定值变化时这种情况下PID控制器输出有很大幅度的跳变,这也是阶跃响应初期瞬时特性变快的主要原因。为了避免设定值变化时控制器输出的大幅度变化,可以选择PI-D形式,即微分只作用于测量值的形式。这种形式也被称为微分先行。当TD=4.25且采用PI-D形式可以避免设定值变化时控制器输出的很大幅度跳变同时改进控制品质。
总体而言适当的增加微分能提高控制系统的稳定性,为了防止设定值变化时PID控制器的输出跳变,可以选择PI-D形式的算法。对于多容特征明显的大时间常数对象使用微分对闭环响应有利,推荐微分时间应为所确定的一系列小的时间常数中的最大值或纯滞后时间的一半,并且不大于积分时间的四分之一。
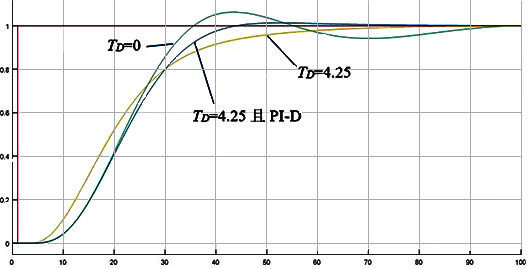
图2 闭环设定值阶跃响应








