分程控制是工程设计中一种常见的控制方式,实际应用中控制效果的好坏与分程点设置有着直接的关系,因此确定分程点也成为分程控制设计中的关键节点。昌晖仪表在本文介绍分程控制的分程点计算和确定方法,希望对仪表工有所帮助。
1、分程控制简述
1.1 分程控制定义
分程控制系统是工业装置中常用的复杂控制系统之一,它不同于一个PID调节器只控制一个调节阀的简单控制系统,而是由一个调节器的输出去带动 2个或2个以上的调节阀。在工业装置中,分程控制的作用主要有2个:一是扩大控制阀的可调范围,以便改善控制的品质;二是为了满足某些工艺操作的特殊需要。
1.2 分程控制的形式
根据分程控制系统中调节阀的开关动作方向的一致性,可将分程控制分为2个主要形式:
第一是分程控制系统中的调节阀开关动作方向相同。当PID调节器输出增大时,各调节阀开度增大,如图1所示;当PID调节器输出增大时,各调节阀开度减小,如图2所示。调节阀同向动作的分程控制系统常用于扩大流量管路阀门可调范围及提高控制质量的应用场合。
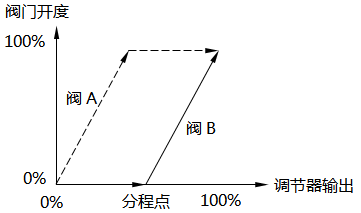
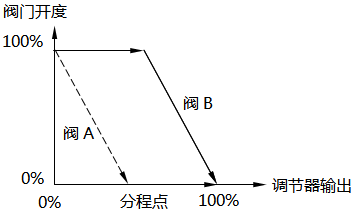
图1 分程控制-阀门同向动作(开度增大) 图2 分程控制-阀门同向动作(开度减小)
第二是分程控制系统中的调节阀开关动作方向相反。当PID调节器输出增大时,一个调节阀开度减小,另一个调节阀开度增大,如图3、图4所示。调节阀异向动作的分程控制系统常用于工艺特殊要求的应用场合。
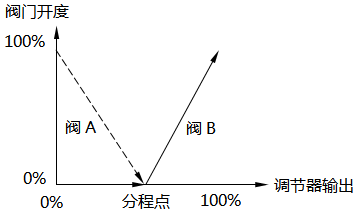
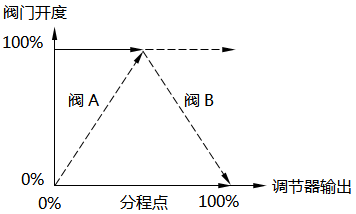
图3 分程控制-阀门反向动作(正V型) 图4 分程控制-阀门反向动作(反V型)
2、仪表工如何计算分程点?
对于分程控制系统,分程点计算就是在PID调节器0-100% 的输出中找到某一点x,使得阀门A在PID调节器0-x%输出段中工作,阀门B在PID调节器x%-100% 输出段中工作,同时点x需使阀A和阀B切换时整个流量管路不出现分程点流量突变,应尽量保持整个系统的流量特性曲线平滑。在实际应用中,分程点的确定大多通过现场试验获取,或者根据同类装置设计经验估算。昌晖仪表将从理论计算的角度推导出分程点的数学公式。
调节阀异向动作的分程控制系统常与工艺特殊操作联系一起,分程点的确定需根据工艺操作要求而定,文中只讨论调节阀同向动作的分程控制系统的分程点计算,为方便描述,约定阀A总是先于阀B调节。
2.1 线性流量系统
对于2个线性流量特性阀门并联组成的分程控制系统,其单个阀门的流量特性为线性,根据《工业控制阀门》IEC60534中阀门线性流量特性的定义,阀门流通能力与阀门开度的计算公式为:
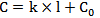 ...........................公式(1)
...........................公式(1)
公式(1)中C为阀门流量系数,k为常数,l为阀门开度(取值为0-1),C0为阀门最小可控流量。
根据线性可叠加原则,并联后管路总流量最大为2个阀门最大流量相加,最小流量为单个阀门最小可调节流量。为计算线性流量特性阀门组成的分程控制系统分程点,推导过程中需忽略并联管路流量特性畸变以及阀门最小可控流量的影响。阀门的最小可控流量会产生不可消除的固有跳变,然而在实际使用过程中,对一般的分程控制系统来说,这个跳变对工艺操作的影响是不大的。A和B两个线性流量特性阀门并联后管路总的流量曲线定义为如下函数:
 ............................公式(2)
............................公式(2)
公式(2)中:C(x)为总管路流量函数;CA和CB分别为阀门A和B的流量函数,且均为线性函数;x为0-1间的变量,对应于阀门0-100%的开度;CA(1)为阀 A最大流量;m为不为零的实数;CB(0)为阀B的最小可控流量,1/m为线性流量系统的分程点。
阀门A和B的切换点需使管路总流量曲线在PID调节器0-100%输出范围内流量调节连续且无突变(忽略最小可控流量引起的跳变),从数学角度分析,即该曲线应连续。
根据函数连续的定义,公式(2)中函数C(x)在点1/m处的极限存在且等于该点的函数值,即可判断该函数连续。
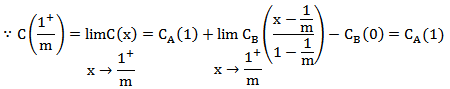
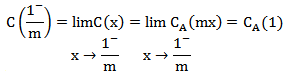
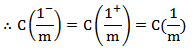
由上述推导可得出管路总流量函数C(x)在0-1封闭区间内连续。
对于并联管路总流量曲线,工艺操作要求该曲线平滑无突变。昌晖仪表选取2个线性流量特性控制阀A和B,最大流量CA,max为200,CB,max为450,可调比R均为50,在PID调节器输出区间选择不同分程点,总管路流量曲线如图5~图7所示。从图5~图7可以看出,图中所示的总流量曲线均连续,而且图6所示曲线在PID调节器输出区间内平滑且调节性能最好。从数学的角度来看图6曲线在调节器输出区间可导,管路系统总的流量特性依然为线性。转换为数学计算也就是对公式(2)求取m值,使得在1/m点处管路总流量函数连续且可导。
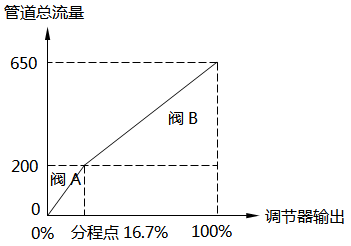
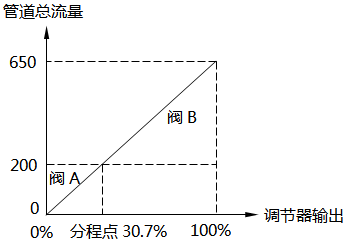
图5 线性流量系统-16.7%分程点 图6 线性流量系统-30.7%分程点
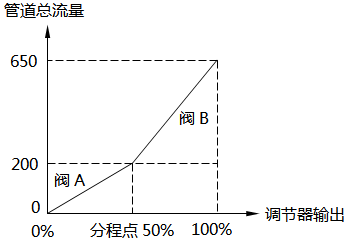
图7 线性流量系统-50%分程点
根据函数可导的定义,函数C(x)在1/m点处可导,即要求函数C(x)连续,同时在1/m点处的左导数和右导数存在且相等。
对于公式(2)中函数C(x),阀门A和B均为线性流量特性,其流量函数均为线性,左导数和右导数均存在。
为求取分程点,令公式(2)中函数C(x)在1/m处的左导数等于右导数,则有:
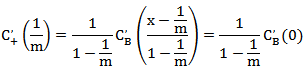


 ..............................公式(3)
..............................公式(3)
公式(3)则为2个线性流量特性阀门组成的分程控制系统的分程点理论计算公式,将该公式应用于前述举例的阀门A和B中,计算分程点。
根据阀门参数及公式(1)可得:
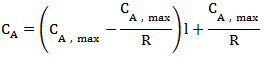
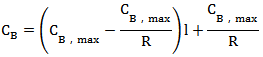
对阀门A和B流量函数求取导数:
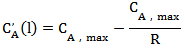
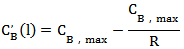
根据公式(3)可计算m值为:
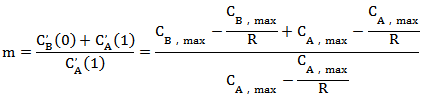 ..............................公式(4)
..............................公式(4)
将阀门参数代入公式(4)中,由此可得分程点1/m为30.7%,总流量特性曲线如图6所示。
该方法在公式推导中忽略了阀门最小可控流量的影响,实际上通过引入修正参数也可以做更严密的推导,但是其计算结果相差很小。文中不列出详细推导过程。
2.2 等百分比阀门管路系统
对于2个等百分比流量特性阀门并联组成的分程控制系统,其单个阀门的流量特性为等百分比,根据《工业控制阀门》IEC60534中阀门等百分比流量特性的定义,阀门流通能力与阀门开度的计算公式为:
 .................................公式(5)
.................................公式(5)
公式(5)中:C为阀门流量系数,k为常数,l为阀门开度(取值为0-1),C0为阀门最小可控流量。
对于2个等百分比阀门并联的分程控制系统分程点的计算,应用类似于线性流量系统的方法,考虑阀门A和B合并后的总管路流量曲线的连续和可导性,经过计算发现该方法并不适用于等百分比系统,因为合并后的总管路流量特性曲线并不可导。这是因为阀A流量曲线为指数函数,从指数函数的图形上可以看出,在PID调节器输出区间内任意点处其右极限数值很大,而阀B流量曲线上的左极限却很小,数值上不可能相等。
为了计算等百分比阀门管路系统的分程点,昌晖仪表引入一种新的工程处理方法。并联管路上的2个阀门A和B均为等百分比流量特性,把该并联管路看成一个整体,工程应用中期望总管路的调节特性也为等百分比。不考虑管路系统流量畸变以及阀门最小可控流量的影响,管路最大调节流量为阀门A和B最大流量的加和,管路最小调节流量为阀门A最小可控流量。根据上述思路,可推导出并联管路的总流量特性曲线。该曲线表征了工艺操作期望的调节特性,也为指数函数,是一条假设的曲线。并联管路实际调节过程分为两段,PID调节器某一区间先调节阀门A开度,阀门B保持开度,而在另一区间,阀门A保持开度,调节阀门B开度。为了使期望的流量曲线与实际调节过程曲线路径偏差最小,通过计算曲线偏差面积,得出并联管路总流量曲线上与阀门A最大流量相等流量值对应的PID调节器输出值即为最优分程点。
昌晖仪表选取2个等百分比流量特性控制阀A和B,最大流量CA,max为200,CB,max为450,可调比R均为50,在PID调节器输出区间使用不同分程点,总管路流量曲线如图8~图10所示。从图中可以看出与90%和50%分程点图相比,当选择76.8%为分程点时,期望曲线(实线)与实际调节流量曲线(点划线)间的面积差最小,且看上去更平滑。
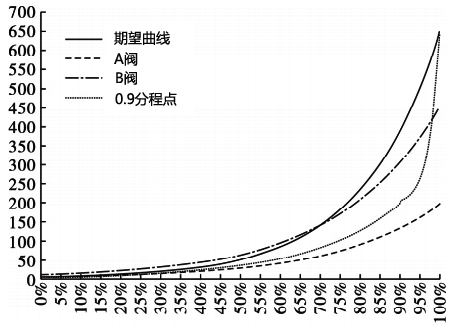
图8 等百分比流量系统-0.9分程点
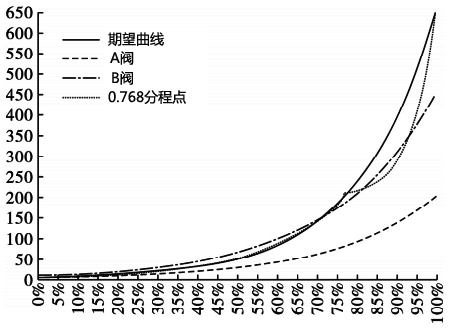
图9 等百分比流量系统-0.768分程点
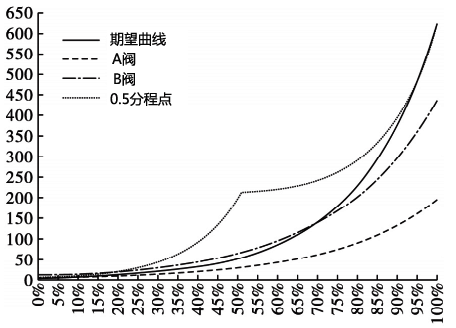
图10 等百分比流量系统-0.5分程点
根据公式(5),阀门A和B的流量特性公式为:

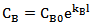
并联管路总流量特性公式为:
 ..............................公式(6)
..............................公式(6)
公式(6)中PID调节器输出为0(0%)时,并联管路中流量为阀门A最小可控流量,即:
 ................................公式(7)
................................公式(7)
公式(7)中PID调节器输出为1(100%)时,并联管路中流量为阀门A和B最大流量的加和,即:
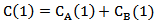 ................................公式(8)
................................公式(8)
将公式(7)和公式(8)代入公式(6) 中可得:
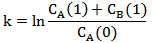

求分程点也即是求点 l0使得:
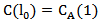 即:
即:
解得:
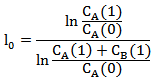 ................................公式(9)
................................公式(9)
实际上,公式(9)中分子CA(1)为阀门A最大流量,CA(0)为阀门A最小可控流量,其比值实际为阀门A的可调比RA。同理,分母CA(1)+CB(1)为并联管路最大流量,也即为阀门A和阀门B的最大流量之和,CA(0)为阀门A最小可控流量,其比值实际为并联管路期望特性流量的可调比R,因此,公式(9)可进一步简化为:
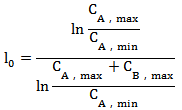 ....................................公式(10)
....................................公式(10)
或
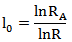 ................................公式(11)
................................公式(11)
公式(10)或公式(11)则为2个等百分比流量特性阀门组成的分程控制系统的分程点计算式,将该公式应用于前述举例的阀门A和B中,计算分程点。
将阀门A和B的参数代入公式(10)或公式(11)中得:

0.768分程点对应的总管路流量曲线图如图9所示。
3、总结
在工程设计中分程控制系统应用非常广泛,但是分程点的确定却是棘手的问题。昌晖仪表通过理论分析,从数学的角度分别给出了线性流量特性和等百分比流量特性阀门并联组成的分程控制系统的分程点计算公式。计算公式非常简单适用,仅需将阀门参数简单代入即可,计算量小,对于提高自控专业工程设计效率有较大的帮助,同时对装置投运过程中分程控制调试具有指导意义。昌晖将该计算方法应用于多个PTA装置设计,与实际运行数据对比,理论计算值与实际运行参数基本一致,达到预期控制效果。
另一方面,关于分程控制分程点计算,还有很多值得研究的问题:昌晖仪表仅提出了2个阀门并联的管路分程点计算,对于3个或更多阀门并联的管路分程点计算还可以做进一步推导;昌晖仪表采用阀门的理论流量曲线做公式推导,对于实际应用的阀门,其流量特性与理论曲线有一定的差别,尤其是偏旋、蝶阀等类型阀门,因此还可通过阀门供货厂商手册或测试采样拟合阀门流量特性曲线,以保证计算值更贴近于实际工况。
关于分控控制的分程点计算及确定方法分享到此结束,如果你需要了解更多分程控制和分程点相关知识,可以在本页面右上角搜索框内输入“分程控制”进行搜索。
作者:冯勇军(硕士,主要从事化工工程设计及自控专业设计)








