一阶纯滞后自衡对象使用三参数描述:稳态增益 K,动态时间 T,纯滞后时间 τ。相应的Lambda整定公式:
比例增益

积分时间

微分时间等于0
一般λ工程上建议大于等于纯滞后时间。如果λ选择小于纯滞后时间会导致有超调的闭环响应,从而使Lambda整定方法的理论基础收到影响。但是实际上现在的整定公式用其他方法也能得到。我们最近通过频域分析在积分时间等于时间常数的情况下得到了非常有意思的结论。

下图是一个τ/T=1/29的时间常数主导对象使用不同λ的闭环阶跃响应。选择不同λ可以实现从过阻尼到等幅振荡的所有闭环响应。

如果被控对象是一个τ/T=29/1的纯滞后主导对象使用不同λ的闭环阶跃响应见下图。选择不同λ可以实现从过阻尼到等幅振荡的所有闭环响应。

λ取值如果使闭环设定值阶跃响应有超调,则λ代表期望闭环时间常数的的工程意义就没有了。但是选择不同的λ仍可以实现时间常数主导对象和纯滞后主导对象闭环响应的一致性。
从更广泛意义上看,选择积分时间等于时间常数后,比例增益应该和时间常数成正比,和增益、纯滞后成反比。想获得不同的闭环性能可以选择不同的系数。这样可能的整定公式可以描述如下。其实a=2超调、a=3临界阻尼,a=3无超调、a=4过阻尼这些都是理论值的近似。而且当a≥2时,(a-1)τ基本上是期望的闭环时间常数。如果a小于2则可以获得有超调的过程。严格意义上的解析解和频域的相位裕度相关,见下表。
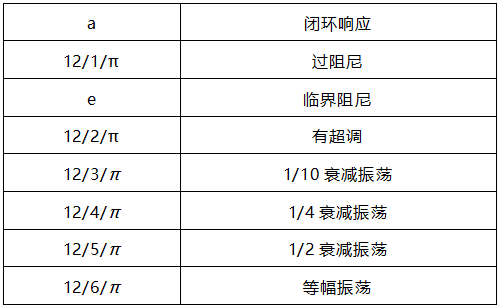
下面这个公式可能是PI参数整定的完整解释。
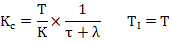
作者:冯少辉博士




