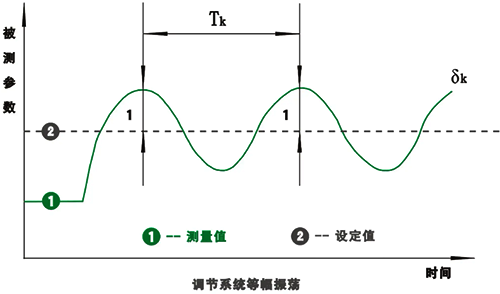
由万老师的这个结论我们做了些研究,得到了几个很有意思的推论:
推论1:纯积分引起的闭环系统等幅振荡,振荡周期一定大于4倍纯滞后,比值越大越靠近4倍纯滞后,比值越小比4倍纯滞后越大。
推论2:Lambda整定如果选择λ=τ,增强比例增益使闭环系统振荡的振荡周期等于4倍纯滞后。
推论3:Lamba整定如果选择λ=τ,比例增益增强π倍闭环系统等幅振荡,这也是其增益裕度。
推论4:Lamba整定如果选择λ=τ,比例增益增强π倍闭环系统等幅振荡。时间常数主导表现为同相位振荡,纯滞后主导表现为异相位振荡。
推论5:Lambda整定方法在纯滞后主导对象时,因为积分时间=时间常数,积分作用太强比例增益必须减小,以获得有超调无振荡的闭环响应。这是其巧妙之处,也是可以进行改进的地方。改进的方法是固定比例增益1/4K的整定方法。




