1942年,在著名的论文“自动控制器的最佳设置”中,泰勒仪器公司销售工程部的J. G. Ziegler和工程研究部的N. B. Nichols提出了两个形成适当控制器参数的程序,开启了现代PID工程整定之路。ZN整定方法有开环和闭环两种。
闭环方法又称为临界比例度方法。分两步:
1、纯比例投用闭环控制回路,确定稳定极限;
2、根据公式计算PID控制器参数。
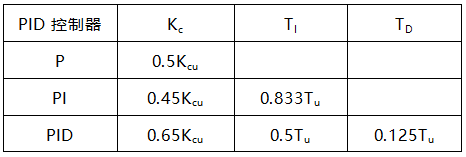
由纯比例控制下的等幅振荡曲线,获得临界控制器增益Kcu与临界振荡周期Tu。并按上表得到正常工作下的控制器参数。
这个方法工程上应用存在三个问题:
①当纯滞后很小时获得等幅振荡的比例增益非常大会超过控制器输出的物理限制;
②使用纯比例让被控对象等幅振荡工业上往往不接受;
③获得振荡的纯比例往往要多次设置,试凑的时间太长也不准确。
但是从临界比例度入手,可以推出一个非常有意思的推论:一阶纯滞后自衡对象比例有界。这个结论很少被人提及,我们是首次发现。如果前人有相似的结论,欢迎大家提供信息。
比例有界1/K
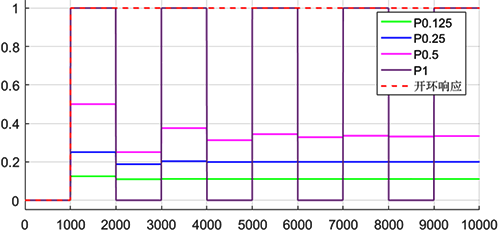
在一个由增益K、时间常数T和纯滞后时间τ确定的一阶纯滞后过程中,获得等幅振荡的纯比例与增益K成反比,与T/τ成正比。如下图所示,同样的纯比例1/2,随着T/τ从5到0闭环响应从无超调,到有超调不振荡再到衰减振荡。

被控对象为纯纯滞后T/τ=0时,获得等幅振荡的纯比例就是所有一阶纯滞后自衡对象稳定控制的比例边界。这个纯比例增益正好等于1/K。这意味着只要纯比例增益小于1/K一定所有的一阶纯滞后自衡对象都能实现稳定控制。
如果希望所有的一阶纯滞后自衡对象都1/4衰减振荡,则工程上的比例边界就可以利用ZN法砍一半设置为1/2K。在现代整定方法中都追求有超调无振荡,则工程上的比例增益边界可以继续砍一半为1/4K。这个比例增益既是所有一阶纯滞后自衡对象的比例边界,也是一个适用于所有一阶纯滞后自衡对象的通解。通解对不同T/τ的响应如下图。
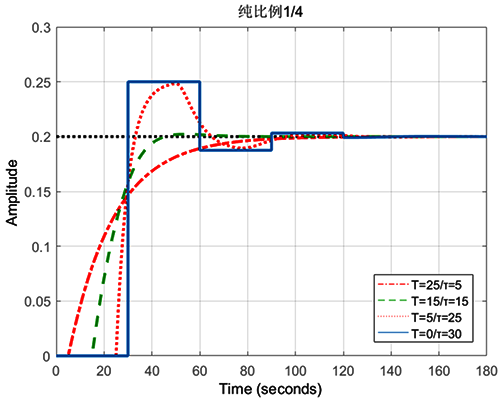
通解魔力在于:实际工业中由于不确定性和耦合影响存在造成的组合自衡对象,只要满足本质单调也普遍适用。当然如果纯滞后较小更大的比例增益可以满足闭环响应有超调无振荡从而改进闭环响应速度。
ZN整定方法中蕴含的这个推论:比例有界,以前没有被发现。如何设置积分作用实现闭环响应有超调无振荡也没有被提出。
作者:冯少辉博士




