表1 自衡和积分对象的特性描述对比


图1 积分对象响应曲线
如图1的积分对象响应曲线所示,对积分对象我们使用响应曲线中过程变量按一定斜率稳定变化后的任一点来确定△PV,从PID控制器输出阶跃变化的起点到该点的时间为τ+△T的总时间。从△PV处沿斜线反向做直线与开始位置的坐标横轴相交,PID控制器输出阶跃变化的起点到该交点为纯滞后时间τ,交点到△PV的时间为△T。
积分对象的增益和自衡对象的增益计算公式一样:

积分对象和自衡对象的特性可以用基本一样的参数进行描述。下面的试验证明:积分对象的Lambda整定方法也可以直接借鉴自衡对象的公式。
为了方便分析,我们定义基准积分对象的模型参数为:稳态系数,增益K=1;动态系数,时间△T=1s;时间滞后,纯滞后时间τ=1s
第一步首先只考虑纯比例控制不考虑积分作用,计算公式与自衡对象的Lambda整定方法类似:

对基准积分对象使用λ=0/τ/3τ=0/1s/3s的设定值阶跃响应曲线,如图2所示。从响应曲线可以看到:λ=τ时过程变量设定值阶跃响应曲线有超调无振荡,是最优闭环响应;如果使用更小的λ,设定值阶跃响应曲线就会振荡,比例作用太强,积分对象也会像自衡对象一样振荡;如果λ=3τ,设定值阶跃响应就会比较缓慢。λ的正确选择应该是基于纯滞后时间。推荐λ≥τ,这个取值范围也和自衡对象的Lambda整定方法类似。

图2 基准积分对象不同λ的设定值阶跃响应
看起来纯比例控制器控制积分对象的效果非常好,积分对象的积分环节可以代替PID控制器的积分作用,实现闭环设定值阶跃响应无稳态余差。但是实际工业应用中,使用纯比例控制器控制积分对象仍存在余差。因为在实际被控对象中干扰的来源多种多样,干扰可能来自被控对象的输出,也可能来自被控对象的输入,这两类干扰引起的余差是不同的。
对图3所示闭环控制系统进行设定值和扰动阶跃变化,其响应曲线如图4所示。设定值阶跃和输出阶跃扰动d₂时纯比例控制器可以实现无余差,但是输入阶跃扰动d₁时纯比例控制器有余差。这就是实际使用中,积分对象虽然已经有积分作用,但是使用纯比例控制器还是有余差的原因。
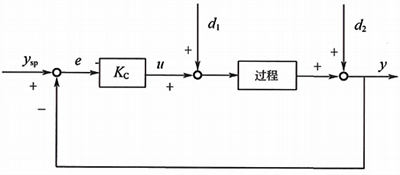
图3 纯比例控制框图

图4 积分对象纯比例控制的设定值、输出扰动、输入扰动的阶跃响应
即使被控对象是积分对象,考虑到扰动的复杂性,为了消除各种扰动可能导致的余差,也推荐使用比例积分控制而不是纯比例控制。
关键是积分时间如何设置才能既避免振荡又能消除余差。积分时间太大,闭环响应不会振荡,但是消除余差的能力会比较弱;反过来积分时间太小,则闭环系统超调加大甚至会振荡。
针对基准积分对象,选择λ=τ,则:

不同积分时间的设定值阶跃响应如图5所示。可以看出:纯比例不振荡,积分作用太强了引起振荡,积分作用弱了消除余差比较慢,增强积分作用闭环响应超调更严重,更容易振荡。增加积分作用后过程变量的超调量明显增加,这是由积分对象的积分作用和比例积分控制器的积分作用的双重作用造成的。最佳的积分时间能最快速消除余差而且还不会引起振荡。

图5 基准积分对象比例积分控制器不同积分时间的设定值阶跃响应
△T会随着在响应曲线上的选点不同而变化,所以△T并不是积分对象的本质特性,不能用于确定积分时间。根据分析知道:对积分对象而言,当使用比例积分控制时,积分时间足够大,比例增益和积分时间的乘积满足式(4-16)时,积分对象不会振荡,这个结论的理论推导见附录。但是积分对象的闭环响应会出现超调,而且基本上一直都有超调。

推荐的不振荡最小积分时间为:
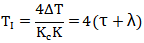
对积分被控对象,使用比例积分控制器的Lambda整定公式:

积分对象的Lambda整定方法可以归纳为:微分不用、积分足够、比例适当。




