自衡被控对象可以用三个参数描述：稳态系数增益K、动态系数时间常数T和纯滞后时间τ。Lambda整定方法使用下面的公式确定自衡对象的PID参数：
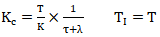
式中，λ为期望的闭环时间常数。
公式
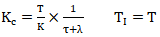和公式
的形式一致，只是把调节闭环性能的参数从τ变成了λ。实际上λ反映了控制回路的期望闭环时间常数。λ越大控制回路的闭环响应速度越慢，λ越小控制回路的闭环响应速度越快。对基准自衡对象使用λ=0/τ/2=τ0s/3s/6s，对应的比例增益分别为0.5/0.25/0.167。从图1的设定值阶跃响应曲线和前面的分析可以看到：λ=τ时过程变量设定值阶跃响应曲线有超调无振荡，是最优闭环响应；λ变小，设定值阶跃响应曲线就会超调加大甚至振荡；如果λ=2τ，设定值阶跃响应就比较缓慢。λ的正确选择应该是基于纯滞后时间而不是时间常数。也有资料说λ的选择是基于时间常数，这也是一个错误的传言。推荐λ≥τ。当λ≥τ后，λ基本上与闭环系统的时间常数相当。
图1 基准自衡对象不同λ的设定值阶跃响应
自衡对象的Lambda整定方法可以归纳为：微分不用、积分固定、比例可调。
自衡对象控制模型计算
在Lambda整定方法确定后，计算PID参数的公式就确定下来了。现在自衡对象PID参数整定的难点就转移到如何获取被控对象的控制模型和如何确定合理的λ上。
对于自衡对象而言，模型增益无论使用开环测试还是闭环测试，其计算公式都一样：
要注意模型增益计算数据可能受到干扰的影响，建议多次测试并选择大的模型增益进行PID控制器参数计算。
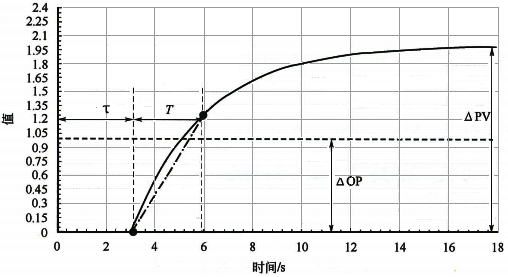
图1 一阶纯滞后自衡对象的控制模型示意图
所谓的自衡对象响应曲线，指的是在自衡被控对象处于稳态时对控制器输出做阶跃变化后的响应曲线。自衡对象特性计算需要知道4个参数△OP、△PV、τ和T。稳态的△OP和△PV可以在响应曲线中很容易获得。63.2%△PV对应的时间为τ+T的时间终点，τ+T的时间起点为控制器输出开始阶跃变化的时间。要在这两个时间中间取一个分割点，从控制器输出开始阶跃变化的起点到这个分割点的时间段为纯滞后时间τ，从这个分割点到τ+T的时间终点的时间段为时间常数T。
通过上面的分析，我们可以把自衡对象基于响应曲线的控制模型的重点放在：如何对从[ID输出开始阶跃变化的起点到τ+T的时间终点这段时间进行分割。最直观准确地确定纯滞后时间τ和时间常数T的分割点的方法是切线法。从响应曲线第一次到达63.2%△PV的位置，沿响应曲线向开始位置的横坐标轴同时向开始方向做响应曲线的切线或交线，切线或交线与开始位置的坐标横轴相交。输出变化到交点为纯滞后时间τ，交点到63.2%△PV的时间为时间常数T。
一阶纯滞后、多容纯滞后、反向过程的自衡对象的控制模型的选取原则分别见图1、图2和图3。这种基于响应曲线获取控制模型的方法是将Lambda整定方法工程化的很重要的创造性工作。
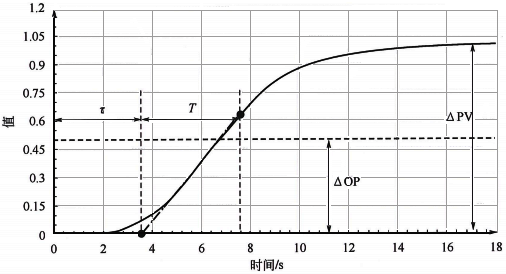
图2 多容纯滞后自衡对象的控制模型示意图
图3 反向自衡对象的控制模型示意图
相关阅读
◆自衡对象和非自衡对象的Lambda整定