图1是不同增益基准自衡对象Kc=0.25时设定值阶跃响应。可以发现:随着被控对象增益的增加,设定值阶跃响应的振荡逐渐加剧。所以最优比例增益应该和被控对象的增益成反比。被控对象增益越大最优比例增益应该越小,反过来被控对象增益越小最优比例增益应该越大。

图1 不同增益基准自衡对象Kc=0.25时设定值阶跃响应
图2是不同时间常数基准自衡对象Kc=0.25时设定值阶跃响应。可以发现:随着被控对象时间常数的增加,设定值阶跃响应越来越缓慢。所以最优比例增益应该和被控对象的时间常数成正比。被控对象时间常数越大最优比例增益应该越大,反过来被控对象时间常数越小最优比例增益应该越小。
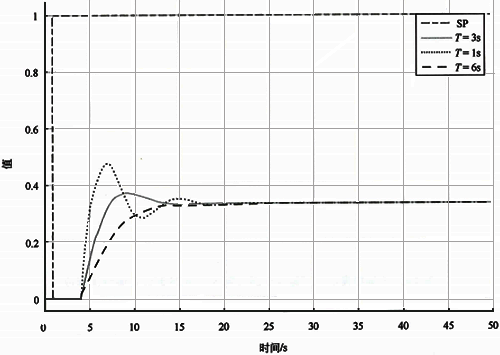
图2 不同时间常数基准自衡对象Kc=0.25时设定值阶跃响应
图3是不同纯滞后时间基准自衡对象Kc=0.25时设定值阶跃响应。可以发现:随着被控对象纯滞后时间的增加,设定值阶跃响应的振荡逐渐加剧。所以最优比例增益应该和被控对象的纯滞后时间成反比。被控对象纯滞后时间越大最优比例增益应该越小,反过来被控对象纯滞后时间越小最优比例增益应该越大。
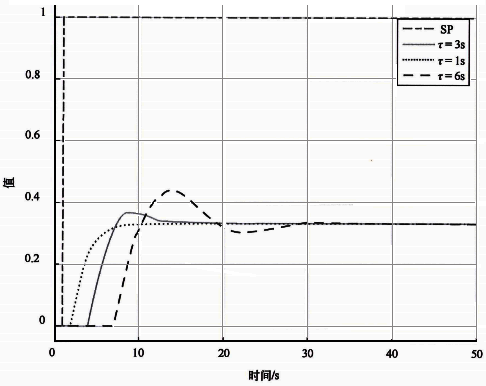
图3 不同纯滞后时间基准自衡对象 Kc=0.25 时设定值阶跃响应
图4是τ/T=1情况下不同时间常数基准自衡对象Kc=0.25时设定值阶跃响应。可以发现:如果被控对象的τ/T=1不变,时间常数和纯滞后时间从1s到12s设定值阶跃响应的形状都基本不变。所以不使用单独的τ或者T反映被控对象控制的难易程度是科学的。一般当τ/T<1时被控对象属于时间常数主导对象,该对象容易控制稳定。当τ/T≥1时被控对象属于纯滞后主导对象,该对象比较难控制稳定。

图4 τ/T=1情况下不同时间常数基准自衡对象K=0.25时设定值阶跃响应




