
图1 纯滞后时间为0基准自衡对象不同Kc的设定值阶跃响应
基准自衡对象采用纯比例控制时的设定值阶跃响应如图2所示。被控对象的纯滞后时间从0s增加到3s后,比例增益Kc=0.1时设定值阶跃响应没有超调,但是比例增益Kc=1时设定值阶跃响应就表现出欠阻尼振荡的特性。随着比例增益Kc的进一步增加,设定值阶跃响应甚至可能发散振荡。
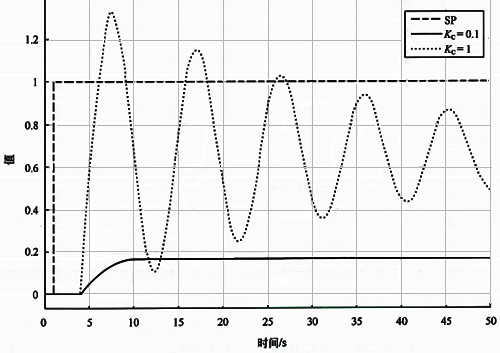
图2 基准自衡对象不同Kc的设定值阶跃响应
实际生产过程中始终都存在纯滞后,所以一般说随着比例作用的增强,设定值阶跃响应会从无超调到有超调无振荡,再到衰减振荡甚至发散振荡。纯滞后时间是控制系统闭环振荡的根源,大纯滞后被控对象纯比例控制器的比例增益要非常小,设定值阶跃响应才能不振荡。纯比例控制器的最优比例增益应和被控对象的纯滞后时间成反比。
图3为基准自衡对象采用纯比例控制器Kc=1的设定值阶跃响应曲线。该衰减振荡响应曲线的过程变量和控制器输出有明显的同相位(同极值同拐点)特性。如果一个控制回路表现出过程变量和控制器输出的同相位振荡而且没有外界干扰的话,往往是比例作用太强引起的。选择将比例作用减半可以改善闭环性能。
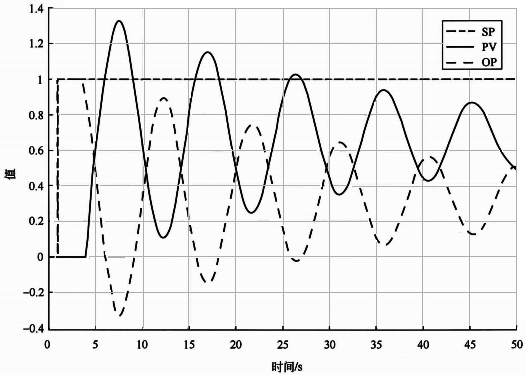
图3 基准自衡对象Kc=1时的设定值阶跃响应
使用纯比例控制器Kc=0.5,基准自衡对象的设定值阶跃响应如图4所示。如果闭环系统是比例作用太强引起的等幅振荡,比例作用减半后系统的设定值阶跃响应会改善为衰减振荡特性。但是这种衰减振荡特性在现代整定观点来看比例作用还是太强。
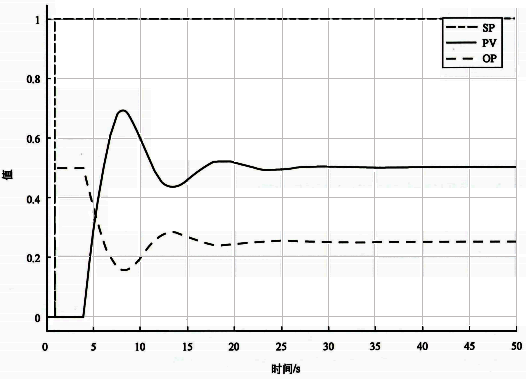
图4 基准自衡对象Kc=0.5时设定值阶跃响应
比例作用再减半为Kc=0.25,基准对象的设定值阶跃响应会是什么样呢?使用Kc=0.25基准自衡对象的设定值阶跃响应,如图5所示。过程变量表现出有超调无振荡的目视最优闭环性能。
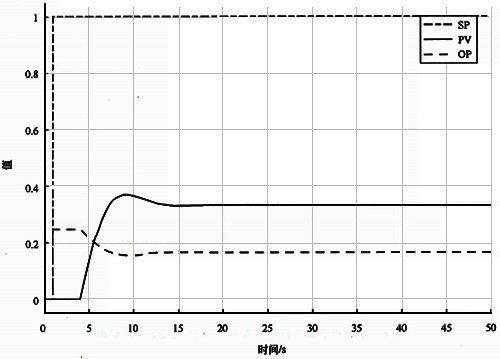
图5 基准自衡对象Kc=0.25时设定值阶跃响应
综上所述,我们可以根据上面的设定值阶跃响应曲线,直观地得到自衡对象最优纯比例控制的认识:
①纯比例控制始终有余差;
②最优比例增益应与纯滞后时间成反比;
③最优比例控制增益足够小则不会振荡;
④最优比例增益太大会引起控制器输出和过程变量的同相位振荡。
请继续阅读:模型特性对控制系统控制性能的影响




