自衡过程
自衡过程的过程变量在输入发生变化时,无需外加任何控制作用,过程能够自发地趋于新的平衡状态。
PID控制器输出的阶跃变化响应,初始过程变量稳定的自衡过程将重新稳定在一个平衡位置,如图1所示。到目前为止我们讨论的所有过程都是自衡过程。

图1 自衡过程阶跃响应曲线
积分过程
积分过程的过程变量在开环情况下仅在平衡点是稳定的,过程变量与过程输入对时间的积分成比例。
积分过程依赖于平衡过程输入和输出来保持稳定。对处于稳定积分过程的PID控制器输出进行阶跃变化,将导致过程变量向一个方向逐渐移动,直到物理限值。图2显示了积分过程的阶跃响应曲线。

图2 积分过程阶跃响应曲线
储罐液位是典型的积分过程。当流入储罐的物料量与流出储罐的物料量相匹配时,过程输入和输出处于平衡状态,储罐液位将保持恒定。如果我们做一个阶跃变化,增加进入储罐的物料流量,过程将失去平衡,储罐液位逐渐上升,直到物料溢出储罐。
积分过程如果处于手动工作模式,很容易受到外界的影响而在某个时刻失控。对生产过程中的任何积分过程,都应该设计控制方案以通过反馈实现过程稳定。
虽然积分过程的响应曲线与自衡过程的响应曲线显著不同,但积分过程仍然可以用和自衡过程纯滞后时间、时间常数和增益类似的参数进行表征。
1、积分过程的纯滞后时间
积分过程的纯滞后时间可以与自衡过程同样的方式测量,纯滞后时间为PID控制器输出变化和过程变量开始变化之间的时间。
2、积分过程的时间
积分过程的特性决定了不能从响应曲线中轻易确定时间常数,因为积分过程没有稳定的过程变量变化。同时PID参数整定方法研究表明:时间常数在积分过程的PID参数整定中并不那么重要。 一个自衡过程的时间常数会提供一个很好的积分时间的参考值,而积分过程只能人为决定不会引起振荡的积分时间。在积分过程响应曲线中使用时间△T 代替时间常数。
对积分对象我们使用过程变量按一定斜率稳定变化后的任一点来确定△PV, 从阶跃测试开始到该点的时间为τ+△T 的总时间,过程变量开始变化的时间到△PV的时间为时间△T。
3、积分过程的增益
△T时间内的△PV与△OP的商作为积分过程的增益。这个增益和△T的比值是个固定值。
4、积分过程表征参数计算
图2是积分过程对控制器输出5%阶跃变化的响应曲线,控制器输出在1s 时改变,直到8s过程变量才开始变化。这个过程的纯滞后时间是:
τ=8-1=7s
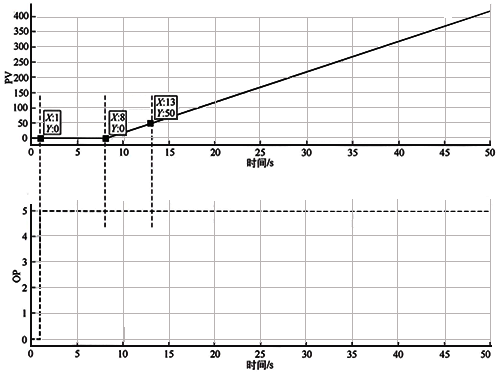
图3 积分过程响应曲线
如图3所示,过程变量从第8s开始变化,从8s到13s过程变量从0到50。积分过程的增益与自衡过程类似,但是因为响应曲线不同,我们现在规定:
△T=13-8=5s
△PV=50-0=50
△OP=5-0=5
K=50/5=10
不管如何选择△T, 计算的K/△T的值恒等于2,这其实是单位阶跃输入变化引起的积分过程的过程变量稳态变化斜率,也称飞升速率。
相关阅读
◆什么是自衡对象和积分对象




