工业中普遍使用PID控制算法,其中90%是PI控制算法。因为自衡对象使用PI控制算法有一致、通解和任意三大特点,这三个特点的发现,标志着我们的Lambda工程整定方法研究基本收官:
1、一致
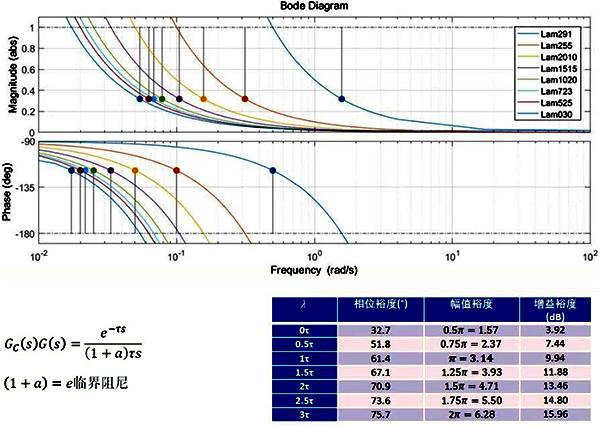
对一阶纯滞后对象。从τ/T=1/29、5/25、10/20、15/15、20/10、25/5、30/0(相当于0.035~∞)按一样的整定规则,总有PI控制参数都能获得一致的幅值裕度和相位裕度。PI控制器从时间常数主导到纯滞后主导再到纯纯滞后都表现出了高度的一致性。稳定裕度也非常漂亮。上面的公式说明一阶纯滞后对象使用PI控制,在经过参数整定后的闭环性能只和纯滞后时间、期望闭环时间常数相关。闭环性能和时间常数或者τ/T无关。不存在PI不适用于大纯滞后的概念。闭环性能只和纯滞后时间相关,当然纯滞后主导后闭环性能会比开环慢。
2、通解
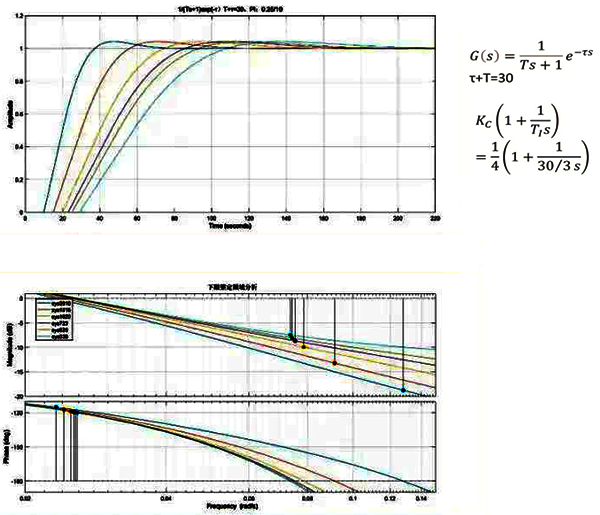
存在适用于所有自衡对象PI控制通解参数:比例增益1/(4K)和积分时间(τ+T)/3。这也意味着对自衡对象PI控制时应该存在最小的比例增益。1.如果比例增益小于1/(4K)系统还是振荡,则肯定是积分作用太强引起的。2.如果比例增益大于1/(4K)系统振荡,模型准确的话1/(4K)和(τ+T)/3就能控制住。这给流量控制的默认参数提供了依据。积分对象使用PI存在双积分作用,通解不适用于积分对象。
3、任意
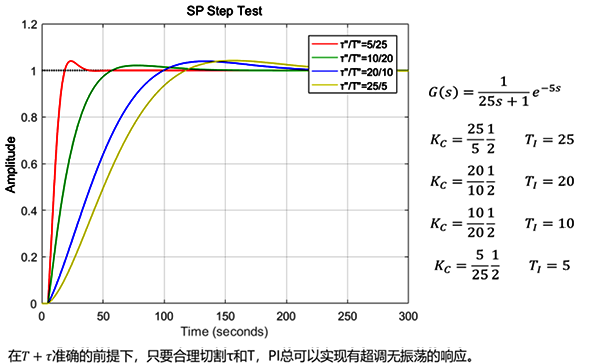
对于一个一阶纯滞后对象。如果T+τ确定。合理切割τ和T就能实现稳定控制。控制使用的等效纯滞后选择的原则是min{τ,(T+τ)*2/3},剩下的就是等效时间常数。这个说明PID整定并不需要知道被控对象的准确模型信息,当然了模型信息越准确闭环性能越好。这并不是否定响应曲线切线切割的重要性,等效纯滞后估计的太小比例会引起振荡,估计的太多往往会损失性能。任意的本质是在大时间常数输出受限时实现有超调无振荡,在纯滞后主导时避免比例增益太小。
对Lambda整定方法的频域分析发现了“一致”。对PID整定是不是基于模型的认识发现了“任意”。对纯滞后主导小比例增益以及纯纯滞后纯积分控制的性能损失发现了“通解”。
作者:冯少辉博士




