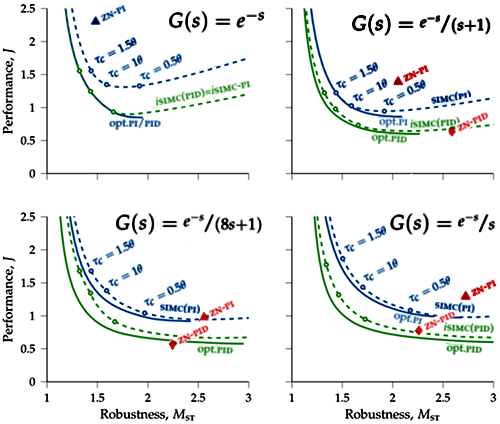
Grimholt博士还有一个非常有意义的研究是关于史密斯预估控制的。我们现在知道纯滞后时间是应用反馈控制时要考虑的一个重要方面,因为它对性能施加了严重的限制。我们主要使用比例积分(PI)控制器,这是过程工业的主力,超过95%的所有控制应用都是这种类型。工业界普遍认为大纯滞后被控对象用PID比较难控制。史密斯预估控制器是最广为人知的针对大纯滞后被控对象的控制器。史密斯预估控制器使用一个没有时间纯滞后的过程模型来预测过程输出,这个新的过程由一个传统的控制器控制,例如PI控制器。史密斯预估控制器消除了闭环传递函数的内部纯滞后具有良好的设定值响应。但是史密斯预估控制器对抗干扰能力非常弱而且对时间延迟的变化非常敏感,甚至更小的时间延迟也可能导致不稳定。有谣言认为PID控制对大纯滞后被控对象控制效果不佳,可能是因为最早的ZN整定方法非常不适用于大纯滞后被控对象。很有意思的结论。PID比史密斯预估控制器更适合大纯滞后被控对象有几个人的研究都有相似的结论,包括Hägglund等。Hägglund提出了预测PI控制算法,但是认为这个算法的改进性能并不明显也是他说的,有意思。




