
一个闭环控制的基本框图如下,我们说一个闭环控制最基本的特点就是具有反馈。而PID则是将输入与反馈的差值进行处理后达到预期输出。
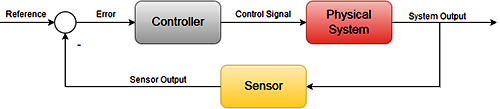
一个稳定系统可能有三种阻尼状态:过阻尼(turquoise line below);临界阻尼((red line below);和欠阻尼(green line below;以及只存在于理想的无阻尼状态((blue line below)。
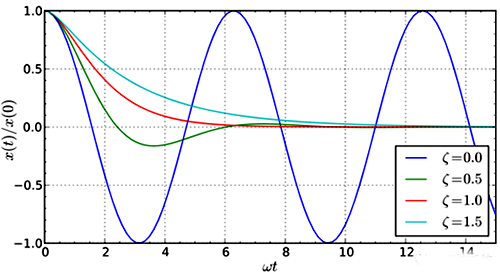
PID是通过不断监测输出与设定的偏差,并对监测到的偏差进行比例、微分、积分处理,并将三个结果整合生成预期输出,偏差为0并一直维持着。这实际上是一个动态平衡,也正是跷跷板理论的切入点:以跷跷板的平衡控制来类比PID控制:本质上都是对偏差的平衡控制。
首先,我们将比例、微分、积分三个环节剥离开来分别进行介绍。
P or Proportional
P-Gain提供对偏差的即时响应,快速将输出拉近至设定值。其数学描述大体如下:
P=ProportionalkP=Proportional Gain|SP=Set point|PV=Process Value|Err=Error
Err=SP-PV
P=kP×Er
因而P的作用随着靠近设定值而不断减弱直至输出与设定重合时降低为零。
过大的P值虽然可以提高快速性但也可能引起振荡失稳,如下图绿线所示。

从跷跷板理论看单纯的P控制是个有差系统,即必须维持一个偏差才能使得跷跷板维持平衡。以刚度来类比。
D or derivative
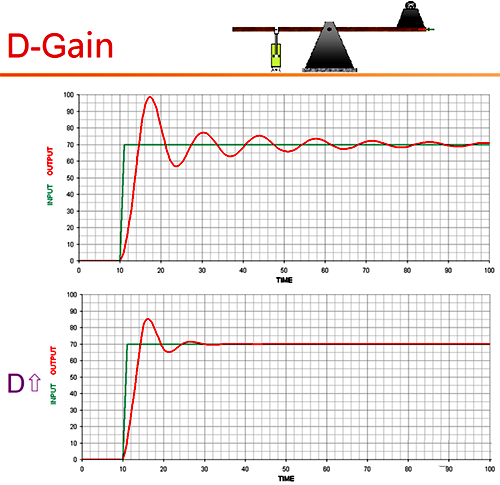
D-Gain主要是提供控制过程的预测;通过对斜率的预测提前介入控制从而减少超调的发生,简单点可以理解成防止过快的控制斜率发生。其数学描述如下:
D=Derivative|kD=Derivative Gain|dt=cycle time of the controller|pErr=Previous Error
D=kD×(Err–pErr)/dt
因而D具有削峰和压制波动的作用。
跷跷板控制理论更是将其作用比喻成阻尼缸,就类似用打气筒的感觉。
I or Integral
I的核心功能是消差。是随着时间周期的每一循环不断累加误差,因而误差越大以及累积的时间越长,积分环节对输出影响的权重就越大。直至误差为零。
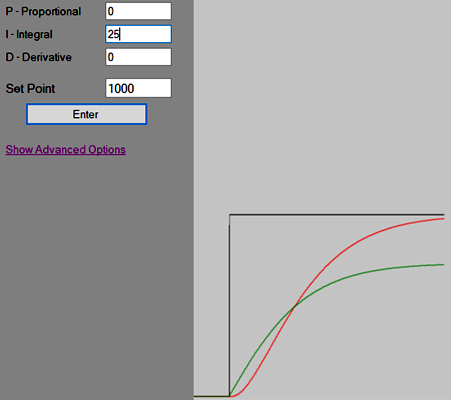
积分的数学描述如下:
I=Integral|kI=Integral Gain|dt=cycle time of the controller|It=Integral Total
I=kI×Err×dt
It=It+I
跷跷板控制理论形象地将积分比喻成了存储误差的容器,装满或到平衡为止。
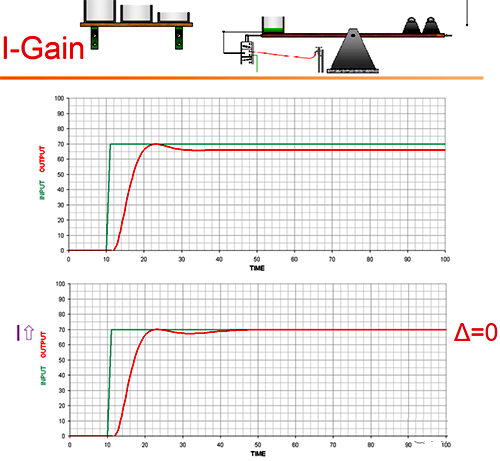
积分环节如同比例环节一样都是在误差越大的时候作用愈大。尤其是在刚给信号或刚上电的控制初期作用十分地迅猛。这也是为什么有些压力控制阀的控制不设积分或增设积分使能的缘故。显然安全是第一位的。
PID合起来的数学描述如下:
Err=Sp–PV
P=kP×PErr
It=It+(Err×kI×dt)
D=kD×(pErr-Err)/dt
pErr=Err
Output=P+It+D
Wait dt (?ms), and perform loop again
PID seasaw合起来如下,实际上还会有一些辅助手段。
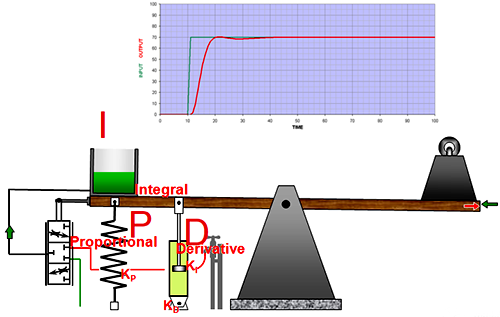
Controlling a system in theory is so much easier than in real life
真实的控制还将面临诸多挑战:来自各种噪音,尤其是传感器;来自加工制造的非理想化;受限于核心部件执行器的分辨率;Δt数字控制无法绕过的火焰山:控制不能连续性的问题。
那么,请仔细思考一下我们该如何来调一个PID闭环控制呢?




