很多轴承的制造商会采用“额定寿命”的概念来给在特定载荷条件下的给定轴承估计一个疲劳耐久性。因为载荷对轴承来说是最重要的需要满足的功能需求。本文给大家介绍轴承额定寿命的概念以及计算的方法,和在计算中需要考虑的其他因素。
对于所有的滚动轴承及来说,额定寿命的计算都可以根据下面的公式来得到:
 。在公式中,P为当量动负荷;C为基本额定动负荷;p为轴承指数,根据滚动体类型的不同,p的值不同。
。在公式中,P为当量动负荷;C为基本额定动负荷;p为轴承指数,根据滚动体类型的不同,p的值不同。从上述的公式就可以看出来,基本额定寿命从根本上讲是一个轴承在实际状态下的载荷与定义出的载荷下的比值。
需要跟大家重复的:
第一,关于当量动负荷(P)的计算公式:P=XFr+YFa
第二,C是跟轴承本事设计相关的参数,它是如下轴承参数的函数:
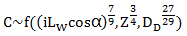
这样计算出来的轴承单位是百万转,也就是轴承能运行的转数。如果知道轴承的转速,我们可以把轴承的寿命转化成运行的小时数,这个也比较符合工业上一般的使用习惯。
其中,公式中的n是轴承的转速。
从上面的公式可以看出来,轴承的基本额定寿命的最主要的基础就是以轴承的载荷为主要计算参数,得到一个轴承实际载荷和额定载荷之间的比值。L10表示的就是90%可靠性下的轴承寿命。h表示这个轴承计算出来的单位是小时,也就是运行的时间。
修正额定寿命
我们都知道,影响轴承寿命的因素很多,不止是轴承的载荷单一的因素,否则轴承的寿命不会向我们前面的文章讲的那么复杂。虽然我们在讨论轴承寿命的时候,最主要讨论的是轴承的载荷,或者说轴承接触时滚道(或者滚动体)的应力。但是从多年的轴承应用经验来说,影响轴承实际运行的还有轴承的润滑,轴承的运行中的污染等等一系列其他的因素。
另外还有挺重要的因素,也是我们在大部分的应用中没有讨论的,轴承的可靠性。
如果要考虑上述的因素,我们就把轴承的寿命公式拓展为:Lnmh=a1a2a3L10h
轴承的可靠性
在大部分的工业应用里,我们讨论的都是90%轴承有效性,或者可靠性下的轴承寿命。在前面我们也讲过,寿命是一个统计学的概念,我们不能计算每一个轴承的真实寿命是多少,在韦布尔模型里,我们讨论的也都是90%的轴承可以运行到的时间,或者说轴承的幸存概率。
那么是否在某些应用里,我们需要去计算更高的可靠性呢?比如在一些要求更严苛的应用里,例如航空航天,高铁等等。
那么这里我们就需要引入另外一个概念,高于90%可靠性的轴承的寿命。简单的举一个例子,如果说在某一个应用里,我们需要计算99%的轴承都要运行的寿命,那么怎么办。
如上面公式中所示,我们引入了第一个参数a1,这个参数代表了轴承的可靠性。当a1=1时,表示这个轴承的运行的可靠性为90%,也就是我们通常意义上说的轴承的基本额定寿命。
当我们要计算99%的轴承可靠性时,Lnmh中的n就为1,同时根据经验公式得到的a1的值为0.25。也就是说,在这个应用中的所有轴承,只有大概四分之一的轴承能够达到99%的可靠性。公式也随之变为:L1mh=0.25a2a3L10h
因为在绝大多数的应用中,我们只考虑轴承90%的可靠性,因此这个参数我们在通常计算时都取1就可以了。除非遇到非常特殊的应用,我们需要考虑更高的可靠性时,您可以跟您的轴承供应商联系,获得相对准确的可靠性参数。另外,这个参数也可以在国际标准(ISO281)中查询。我们这里就不多做介绍了。
除了可靠性系数以外,我们看到在修正系数里还有两个参数a2,a3,这两个参数在国际标准或者绝大多数的轴承供应商那里目前都被aISO所取代。
这个修正系数考虑了下列因素的影响:
①轴承载荷,
②润滑条件(包括润滑剂的类型,粘度,转速,轴承尺寸,添加剂等等)
③材料的疲劳极限
④轴承类型
⑤材料的残余应力
⑥环境条件(污染系数)
关于轴承额定寿命的知识就分享到这里。上面谈到的这些系数对轴承寿命的影响如何,昌晖仪表在随后的文章中跟大家继续讨论。




