1、测量范围、上下限及量程
每个用于测量的仪表都有测量范围,它是该仪表按规定的精度进行测量的被测变量的范围。测量范围的最小值和最大值分别称为测量下限和测量上限,简称下限和上限。仪表的量程可以用来表示其测量范围的大小,是其测量上限值与下限值的代数差,即:仪表量程=测量上限值-测量下限值。 使用下限与上限可完全表示仪表的测量范围,也可确定其量程。如一个温度测量仪表的下限值是-50℃,上限值是 150℃,则其测量范围可表示为-50℃~150℃,量程为 200℃。由此可见,给出仪表的测量范围便知其上下限及量程,反之只给出仪表的量程,却无法确定其上下限及测量范围。
2、零点迁移和量程迁移
仪表测量范围的另一种表示方法是给出仪表的零点即测量下限值及仪表的量程。由前面的分析可知,只要仪表的零点和量程确定了,其测量范围也就确定了。因而这是一种更为常用的表示方式。在实际使用中,由于测量要求或测量条件的变化,需要改变仪表的零点或量程,为此可以对仪表进行零点和量程的调整。通常将零点的变化称为零点迁移,而量程的变化则称为量程迁移。
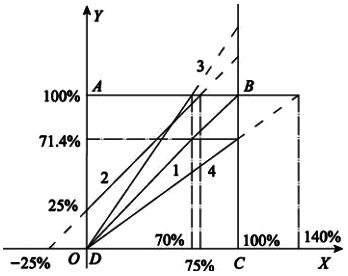
图1 仪表零点迁移和量程迁移示意图
以被测变量值相对于量程的百分数为横坐标,记为X,以仪表指针位移或转角相对于标尺长度的百分数为纵坐标记为Y,可得到仪表的标尺特性曲线X-Y。假设仪表标尺是线性的,其标尺特性曲线可如图1中的线段1所示。
考虑单纯的零点迁移情况,如线段2所示,此时仪表量程不变,其斜率亦保持不变,线段2只是线段1的平移,理论上零点迁移到了原输入值的-25%,终点迁移到了原输入值的75%,而量程则仍为100%。考虑单纯的量程迁移情况如线段3所示,此时零点不变,线段仍通过坐标系原点,但斜率发生了变化,理论上量程迁移到了原来的70%。
由于受仪表标尺长度和输入通道对输入信号的限制,实际的标尺特性曲线通常只限于正四边形ABCD内部,即用实线表示部分;虚线部分只是理论上的结果,无实际意义。因此,线段2的实际效果是标尺有效使用范围迁移到原来的25%-100%,测量范围迁移到原来的0-75%。线段3的实际效果是标尺仍保持原来有效范围的 0~100 %,测量范围迁移到了原来的0-70%。同理,考虑图中线段4所示的量程迁移情况,其理论上零点没有迁移,量程迁移到原来的140%;而实际上标尺只保持了原来有效范围的 0-71.4%,测量范围则仍为原来的0-100%。
零点迁移和量程迁移可以扩大仪表的通用性。但是,在何种条件下可以进行迁移能够有多大的迁移量,还需视具体仪表的结构和性能而定。
3、灵敏度和分辨率
灵敏度是仪表对被测参数变化的灵敏程度,常以在被测参数改变时,经过足够时间仪表指示值达到稳定状态后,仪表输出变化量△Y与引起此变化的输入变化量△U 之比表示,即:灵敏度=△Y÷△U。可见,灵敏度也就是图1所示标尺特性曲线的斜率。因此,量程迁移就意味着灵敏度的改变,而如果仅仅是零点迁移则灵敏度不变。
由灵敏度的定义表达式可知,灵敏度实质上等同于仪表的放大倍数。只是由于U和Y都有具体量纲,所以灵敏度也有量纲,且由U和Y确定;而放大倍数没有量纲。所以灵敏度的含义比放大倍数要广泛得多。
仪表工常容易将仪表灵敏度和仪表分辨率混淆。仪表灵敏限是仪表输出能响应和分辨的最小输入量;分辨率是灵敏度的一种反映,一般说仪表的灵敏度高,则其分辨率同样也高。因此实际中主要希望提高仪表的灵敏度,从而保证其分辨率较好。在由多个仪表组成的测量或控制系统中,灵敏度具有可传递性。例如首尾串联的仪表系统(即前一个仪表的输出是后一个仪表的输入),其总灵敏度是各仪表灵敏度的乘积。
4、误差
仪表指示装置所显示的被测值称为示值,它是被测真值的反映。严格地说,被测真值只是一个理论值,因为无论采用何种仪表测到的值都有误差。实际中常将用适当精度的仪表测出的或用特定的方法确定的约定真值代替真值。例如使用国家标准计量机构标定过的标准仪表进行测量,其测量值即可作为约定真值。
示值与公认的约定真值之差称为绝对误差,即:绝对误差=示值-约定真值。 绝对误差通常可简称为误差。当误差为正时表示仪表的示值偏大,反之偏小。
绝对误差与约定真值之比称为相对误差,常用百分数表示,即:相对误差=绝对误差÷约定真值
虽然用绝对误差占约定真值的百分数来衡量仪表的精度比较合理,但仪表多应用在测量接近上限值的量,因而用量程取代式中的约定真值则得到引用误差如式所示:引用误差(%)=绝对误差÷量程。考虑整个量程范围内的最大绝对误差与量程的比值,则获得仪表的最大引用误差为:最大引用误差(%)=最大绝对误差÷量程。最大引用误差与仪表的具体示值无关,可以更好地说明仪表测量的精确程度。最大引用误差基本是误差的主要形式,仪表的主要质量指标之一。
仪表在出厂时要规定引用误差的允许值,简称允许误差。若将仪表的允许误差记为Q,最大引用误差记为Qmax则两者之间满足如下关系Qmax≤Q。
任何测量都是与环境条件相关的,这些环境条件包括环境温度、相对湿度、电源电压和安装方式等。仪表应用时应严格按规定的环境条件即参比工作条件进行测量,此时获得的误差称为基本误差;因此如果在非参比工作条件下进行测量,此时获得的误差除包含基本误差外,还会包含额外的误差,又称附加误差,即:误差=基本误差+附加误差
以上的讨论基本针对仪表的静态误差,静态误差是指仪表静止状态时的误差,或被测量变化十分缓慢时所呈现的误差,此时不考虑仪表的惯性因素。仪表还存在有动态误差,动态误差是指仪表因惯性迟延所引起的附加误差,或变化过程中的误差。仪表静态误差的应用更为普遍。
5、精确度
任何仪表都有一定的误差。因此,使用仪表时必须先知道该仪表的精确程度,以便估计测量结果与约定真值的差距,即估计测量值的大小。仪表的精确度通常是用允许的最大引用误差去掉百分号(%)后的数字来衡量的。
模拟式仪表的精确度一般不宜用绝对误差(测量值与真实值的差)和相对误差(绝对误差与该点的真实值之比)来表示,因为前者不能体现对不同量程仪表的合理要求,后者很容易引起任何仪表都不能相信的误解。例如,对一只满量程为100mA的电流表,在测量零电流时,由于机械摩擦使表针的示数略偏离零位而得到0.2mA的读数,若按上述相对误差的算法,那么该点的相对误差即为无穷大,似乎这个仪表是完全不能使用的;但在工程人员看来,这样的测量误差是很容易理解的,根本不值得大惊小怪,它可能还是一只比较精密的仪表呢!模拟式仪表的合理精确度,应该以测量范围中最大的绝对误差和该仪表的测量范围之比来衡量,这种比值称为相对(于满量程的)百分误差。例如某温度计的刻度由-50℃~200℃,即其测量范围为250℃,若在这个测量范围内,最大测量误差不超过2.5℃,则其相对百分误差δ为:δ=25÷(50+200)=1.0%。
按仪表工业规定,仪表的精确度划分成若干等级,简称精度等级,如 0.1级、0.2级、0.5级、1.0级、1.5级、2.5级等。由此可见,精度等级的数字越小,精度越高。
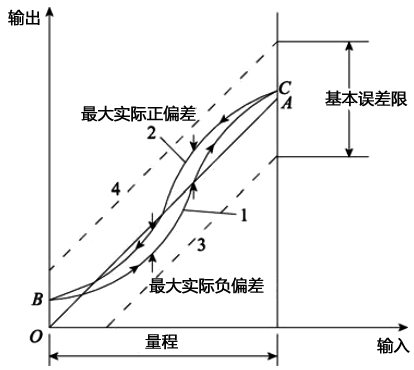
图2 仪表精度定级确定示意图
仪表精度等级的确定过程如图2所示。为便于观察和理解,对其中的偏差做了有意识地放大。图中直线O且是理想的输入输出特性曲线,虚线3和4是基本误差的下限和上限。在检定或校验过程中所获得的实际特性曲线记为曲线1和2,其中曲线1是输入值由下限值到上限值逐渐增大时获得的,称为实际上升曲线;而曲线2是输入值由上限值到下限值逐渐减小时获得的,称为实际下降曲线。由曲线1和2与直线OA的偏差可分别得到最大实际正偏差和负偏差。可见,曲线1和2愈接近直线OA,即仪表的基本误差限愈小,仪表的精度等级越高。
6、滞环、死区和回差
仪表内部的某些元件具有储能效应,例如弹性变形、磁滞现象等,其作用使得仪表检验听得的实际上升曲线和实际下降曲线常出现不重合的情况,从而使得仪表的特性曲线形成环状,如图3所示。该种现象即称为滞环。显然在出现滞环现象时,仪表的同一输入值常对应多个输出值,并出现误差。
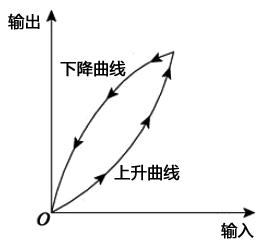
图3 仪表滞环效应分析
仪表内部的某些元件具有死区效应,例如传动机构的磨合间隙等,其作用亦可使得仪表检验所得的实际上升曲线和实际下降曲线常出现不重合的情况。这种死区效应使得仪表输入在小到一定范围后不足以引起输出的任何变化,而这一范围则称死区。考虑仪表特性曲线呈线性关系的情况,其特性曲线如图4所示。因此,存在死区的仪表要求输入值大于某一限度才能引起输出的变化,死区也称为不灵敏区。理想情况下,不灵敏区宽度是灵敏限的2倍。
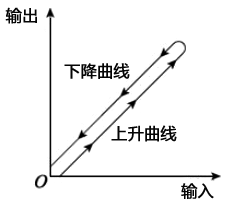
图4 仪表死区效应分析
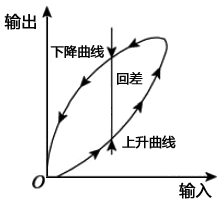
图5 仪表综合效应分析
也可能某个仪表既具有储能效应,也具有死区效应,其综合效应将是以上两者的结合,典型的特性曲线如图5所示。在以上各种情况下,实际上升曲线和实际下降曲线间都存在差值,其最大的差值称为回差,亦称变差,或来回变差。
7、重复性和再现性
在同一工作条件下,同方向连续多次对同一输入值进行测量所得的多个输出值之间相互一致的程度称为仪表的重复性,它不包括滞环和死区。例如,在图6中列出了在同一工作条件下测出的仪表的3条实际上升曲线,其重复性就是指这三条曲线在同一输入值处的离散程度。实际上,某种仪表的重复性常选用上升曲线的最大离散程度和下降曲线的最大离散程度两者中的最大值来表示。
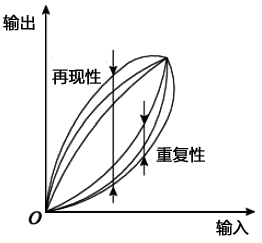
图6 仪表复现性和再现性分析
再现性包括滞环和死区,它是仪表实际上升曲线和实际下降曲线之间离散程度的表示,常取两种曲线之间离散程度最大点的值来表示,如图6所示。
重复性是衡量仪表不受随机因素影响的能力,再现性是仪表性能稳定的一种标志,因而在评价某种仪表的性能时常同时要求其重复性和再现性。重复性和再现性优良的仪表并不一定精度高,但高精度的仪表一定有很好的重复性和再现性。
8、可靠性
表征仪表可靠性的尺度有多种,最基本的是可靠度。它是衡量仪表能够正常工作并发挥其功能的程度。简单地来说,如果有 100台同样的仪表,工作9000h后约有99台仍能正常工作,则可以说这批仪表工作9000h的可靠度是99%。
可靠度的应用亦可体现在仪表正常工作和出现故障两个方面。在正常工作方面的体现是仪表平均无故障工作时间。因为仪表常存在的修复多是容易的,因而以相邻两次故障时间间隔的平均值为指标,可很好表示平均无故障工作时间。在出现故障方面的体现是平均故障修复时间,它表示的是仪表修复所用的平均时间,由此可从反面衡量仪表的可靠度。
基于以上分析,综合考虑常规要求,即在要求平均无故障工作时间尽可能长的同时,又要求平均故障修复时间尽可能短。为综合评价仪表的可靠性,引出综合性指标有效度,其定义为:





