量纲是指“给定量与量制中各基本量的一种依从关系，它用与基本量相应的因子的幂的乘积去掉所有数字因子后的部分表示”。
因子的幂就是按指数增加的因子。每个因子是一个基本量的量纲。基本量量纲的约定符号用单个大写正体罗马字母表示。在国际量制(ISQ)中，基本量的量纲符号见下表。
基本量 长度 质量 时间 电流 热力学温度 物质的量 发光强度
基本量量纲 L M T I Θ N J
导出量量纲的约定符号是由该导出量定义的基本量量纲的幂的乘积表示。量Q的量纲表示为dimQ。例如在国际量制中，力(量的符号F)的量纲表示为
；在同一量制中，
是成分B的质量浓度的量纲，也是质量密度(体积质量)的量纲；长度为l的摆在当地自由落体加速度为g处的周期T是：
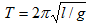或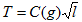
，式中*g，因此，
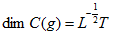。由此，量Q的量纲为
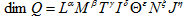，其中的指数a、β、γ、δ、ε、ξ、η称为量纲指数，可以是正数、负数或零。在导出某量的量纲时不考虑标量、向量或张量特性。量纲仅表示量的构成，而不能充分说明量的内在联系。例如在给定量制中，同种量的量纲一定相同，但具有相同量纲的量却不一定是同种量。如在国际单位制中，功和力矩的量纲相同，都是
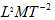，但它们是完全不同性质的量。量纲的意义在于定性地表示量与量之间的关系，尤其是基本量和导出量之间的关系。通过量纲可以得出任何一个量与基本量之间的关系，以及检验量的表达式是否正确。如果一个量的表达式正确，则其等号两边的量纲必然相同，通常称为“量纲法则”。