1、临界震荡过程
控制系统在外界干扰作用后,不能恢复到稳定的平衡状态,而出现一种既不衰减,也不发散的等幅振荡过程,这样的过渡过程就称为临界振荡过程,如图1所示。我们在临界比例度法整定中,首先需要得到的就是临界参数,即在临界状态下,被控量y来回振荡一次所用时间,称为临界周期Tk;被调参数处于临界状态时的比例度,称为临界比例度δk。
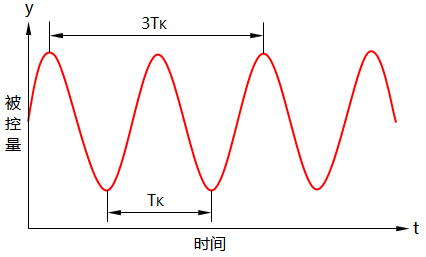
图1 临界振荡过程示意图
用临界比例度法整定PID参数时,要在纯比例作用下,在控制系统中由大到小的改变调节器的比例度,来诱发出过程控制回路中的等幅振荡,得到如图1所示的临界振荡过程,以得到我们所需要的临界比例度δk和临界周期Tk的数值。然后再根据经验公式,计算出调节器各参时间数的具体数值。
2、临界比例度法整定口诀
临界整定应用多,纯P运转减参数;
等幅振荡出现时,δk值Tk值为临界;
按照公式乘系数,P、I、D序不能错;
静观运行勤调整,细心寻求最佳值。
3、临界比例度法整定步骤
云南昌晖仪表制造有限公司结合口诀介绍临界比例度法的整定步骤。
①先把积分时间放至最大微分时间放至零,比例度放至较大的适当值。“纯P转减参数”,就是使控制系统按纯比例作用的方式投入运行。然后慢慢地减少比例度,在外界干扰的作用下,细心观察调节器的输出信号和被调参数的变化情况;如果控制过程的曲线波动是衰减的,则把比例度继续调小,如果控制过程的曲线波动是发散的,则应把比例度调大些,直到曲线波动呈等幅振荡为止,以此得到临界振荡过程,从而得到临界比例度δk和临界周期Tk值。即口诀说的“等幅振荡出现时,δk值Tk值为临界”。
②“按照公式乘系数”即根据得到的δk和Tk值按表1临界比例度法参数计算公式表,来计算调节器的各参数值。
表1 临界比例度法参数计算公式表
调节规律 比例度δ/% 积分时间Ti/min 微分时间Td/min
P 2δk
PI 2.3δk 0.85Tk
PID 1.78δk 0.5Tk 0.125Tk
③求得具体的数值后,将比例度调在比计算数值大一些的刻度上,然后把积分时间放至计算值上,然后从大到小地调整积分时间,最后把微分时间放至计算值上,从小到大地调整微分时间。这样的调整次序就是口诀中的“PID序不能错”。
④最后把比例度减小到计算值上,通过观察曲线,也就是“静观运行勤调整,细心寻求最佳值”。即适当地进行各参数的微调,以达到满意的控制效果。
4、临界比例度法整定PID参数注意事项
①临界比例度很小时将近似于位式控制,这时应注意并观察调节阀门的开、关状态,因为调节阀一会全开,一会全关这对生产是不利的,如燃油锅炉熄火可能会导致爆炸事故的发生。这样的场合尽量把比例度调大一点,而且在寻找临界状态时,要格外小心。否则只有改用其他整定方法。
②工艺对生产参数有严格要求时,如果被调参数出现等幅振荡,可能会影响到生产或安全。这样的对象最好改用其他的整定方法。
③有的对象在整定中,可能会遇到系统临界比例度很小,已把比例度调至10%以下了,但还是不出现临界状态,这时,可采取在5%-10%之内选定一个比例度作为δk的参考值,来进行整定。
④观察临界振荡过程曲线用DCS操作站的显示是很方便的,对于没有使用DCS的场合,可使用无纸记录仪的记录曲线。可采取缩小仪表量程,减小无纸记录仪记录间隔,读取多个周期求平均值的方法,如图1中用3Tk来提高临界振荡过程曲线数值的准确性。
为方便大家学习和提高PID参数整定水平,本站分享一本白志刚老师编写的《自动调节系统解析与PID整定》供您阅读,助您迅速成为PID控制高手!!





